Modeling the Role of the Astrocyte Syncytium and K+ Buffering in Maintaining Neuronal Firing Patterns

 

For many years, glial cells were considered to merely provide structural support, with no relevant contribution to cognitive functions. However, numerous studies over the past decade have demonstrated that glial cells are active players in signal processing and there is now little doubt that advanced brain function is achieved through dynamic interactions among neuronal and glia networks. Among glial cells, astrocytes are believed to perform many functions, including maintenance of extracellular ion balance, control of cerebral blood flow, modulation of synaptic transmission, and neurotransmitter uptake and release (Iadecola & Nedergaard, 2007; Barres, 2008; Newman, 2003; Giaume et al., 2010; Kouji & Newman, 2004; Attwell et al., 2010; Nedergaard et al., 2003). Several studies have demonstrated that astrocytes may play a critical role in the modulation of neuronal network activity, including oscillations and synchronization, mainly through their role in ion homeostasis and uptake of the neurotransmitters GABA and glutamate (Bellot-Saez et al., 2017; Poskanzer & Yuste, 2016; Szabo et al., 2017, Pannasch et al., 2011; Amiri et al., 2013; Chever et al., 2016; Haydon & Carmignoto, 2016). Finally, alterations in normal astrocytic physiology have been associated with several neuropsychiatric, neurodevelopmental, and neurodegenerative diseases, including epilepsy, stroke, Rett syndrome and Alzheimer’s disease (Allaman et al. 2011; Barres, 2008; Chen & Swanson, 2003; Kimelberg & Nedergaard, 2010; Nedergaard & Dirnagle, 2005; Somjen, 2001). 

An important role of astrocytes is to maintain a nearly constant extracellular K+ concentration in the face of neuronal activity that would tend to increase it (Kofuji & Newman, 2004; Bellot-Saez et al., 2007; Ransom 1996; Muller 1996). Failure of astrocytes to maintain proper extracellular K+ concentrations has been implicated in neurological diseases such as epilepsy and stroke (Dirnagl et al., 1999; Kimelberg & Nedergaard, 2010; Moskowitz et al., 2011; Nakase et al., 2003; Zhao & Rempe, 2010). A basic hypothesis for extracellular  K+ clearance, or K+ spatial buffering, was introduced more than a half century ago (Kofuji & Newman, 2004; Orkand et al., 1966). However, recent experiments have demonstrated that astrocyte gap junction coupling may play a crucial role in extracellular ion homeostasis (Ma et al., 2016). In brief, strong gap junction coupling provides isopotentiality to the astrocytic network by minimizing the membrane potential depolarization that follows increased levels of K+; this, in turn, maintains a strong K+ inward driving force, which is critical for efficient astrocytic control of brain homeostasis. The syncytial isopotentiality also provides a stronger and sustained driving force for interastrocyte spatial transfer through gap junction channels and a sustained driving force for K+ release. 

In this study, we develop computational models for two neuron/astrocyte networks to explore mechanisms underlying the astrocytes’ role in maintaining neuronal firing patterns. For the first network, a single neuron receives periodic excitatory inputs at varying frequencies. We consider the role played by several astrocytic dendritic processes, including the Na+- K+  ATPase pump, K+ channels and gap junctions in maintaining extracellular ion homeostasis so that the neuron can faithfully sustain spiking in response to the excitatory input. The second network includes two neurons coupled through mutual inhibitory synapses. Here we consider the role of astrocytic dendritic processes in maintaining anti-phase or synchronous oscillations. 

A primary goal of this paper is to mathematically study the dependence of network behavior on various model parameters and cellular processes. This is done using dynamical systems methods, including bifurcation theory and fast/slow analysis, to systematically reduce the complex model to a simpler set of equations. In fact, we reduce the first network, consisting of differential equations for the neuron and astrocyte membrane potentials, channel state variables and intracellular and extracellular Na+ and K+ concentrations, to a one dimensional map. Fixed points of the map determine whether the astrocyte can maintain extracellular K+ homeostasis so the neuron can respond to periodic input. 

 

 

We consider two neuron/astrocyte network models. Each cell is modeled as a single compartment using the Hodgkin-Huxley formalism (Ermentrout & Terman, 2010). There are equations for the membrane potentials and ionic currents, as well as equations for Na+ and K+ concentrations both inside the cells and in the shared extracellular space. There are also equations for the neuronal and astrocytic Na+-K+ ATPase pumps. Simulations of the model were done using the numerical software XPPAUT (Ermentrout, 2002). 

 

 

The first network consists of a single neuron that receives periodic excitatory input. The neuron is coupled to a single astrocyte through a shared extracellular space. The astrocyte is coupled to other astrocytes through gap junctions. 

 

Neuron: The neuron’s membrane potential, VN, satisfies the equation

\(C_m \frac{dV_N}{dt}=-I_{Na}-I_K-I_{PN}-I_{exc}\) (1)

The first two terms on the right hand side of this equation correspond Na⁺ and K⁺ currents. These are defined as 

\(I_{Na}=(g_{Na} m_∞^3 (V_N )h+g_{NaL} )(V_N-E_{Na} )\)

\(I_K=(g_k n^4+g_{KL} )(V_N-E_K )\)

Note that there are both Na⁺ and K⁺ leaks. As in (Huguet et al., 2016), we assume that h = 1 − n and n satisfies a differential equation of the form

 \(\frac{dn}{dt}=ϕ(n_∞ (V_N )-n)/τ_n (V_N)\) (2)

If X = m or n, then

 \(X_∞ (V)=\frac{1}{1+e^{-(V-θ_X)/σ_x }}\) and \(τ_n (V)=τ_0+\frac{τ_1-τ_1}{1+e^{-(V-θ_n0)/σ_n0 }}\)   (3)

The Nernst potentials are given by

\(E_K=\frac{RT}{F} ln \frac{K_e}{K_i}\)  and  \(E_{Na}=\frac{RT}{F} ln \frac{Na_e}{Na_i} \) (4)

where R,T and F are the gas constant, temperature and Faraday’s constant, respectively, and K_i, K_e, Na_i and Na_e are the K⁺ and Na⁺ concentrations in the neuron’s cytosol and extracellular space.

As in (Kager et al., 2002) the Na⁺-K⁺ ATPase pump current is given by

\(I_{PN}=ρ_N (\frac{K_e}{2+K_e })^2 (\frac{Na_i}{7.7+Na_i} )^3\)   (5)

where r_N represents the maximal pump current.

 

The term I_exccorresponds to periodic, excitatory synaptic input and is given by

\(I_{exc}=g_{exc} s(t)(V_N-E_{syn}) .\)

Suppose that the input is at f_r hz. For each integer j and t_j = j* f_r /1000, we let s(t_j) = 1 and

s’(t) = -b s(t)    for   t_j  <  t  <  t_j+1.

The neuron model parameters are: C_m = 1 mF/cm², g_Na = 20, g_K = 3, g_NaL = .03, g_KL = .2, j = .1, q_m = -37, s_m = 10, s_n = 10, q_n = -55, t₀ = .1, t₁ = 1, q_n0 = -40, s_n0 = -12, g_exc = 2, b = 1 ms^-1. Units for the maximal conductances (g’s) are mS/cm² and half activation variables (q’s) are mV.

 

Astrocyte: The astrocyte’s membrane potential, V_A,  satisfies the equation

\(C_m^A \frac{dV_A}{dt}=-I_K^A-I_{Kir}-I_{Na}^A-I_{P}A-I_{gap}.\)  (6)

where  \(C_m^A\)= 1u\(\)F/cm² and \(I_K^A\) and \(I_Na^A\) correspond to K⁺ and Na⁺ leak currents; these are given by

\(I_K^A=g_K^A (V_A- E_K^A) \)  and  \(I_{Na}^A=g_{Na}^A (V_A- E_{Na}^A)\)

The term I_Kir corresponds to an inward rectifying K⁺ current (Ransom, 1996), and is given by

\(I_{Kir}=g_{Kir} \left({\frac{K_e^{1/2}}{1+e^{(V_A-E_K^A)/19.2}}}\right)(V_A-E_K^A)\)   (7)

The Nernst potentials, \(E_K^A \) and \(E_{NA}^A\), as well as the ATPase pump current I_PA, are defined very similar to (4) and (5).

The term I_gap corresponds to electrical coupling with another astrocyte that is electrically coupled with other astrocytes within a syncytium. We assume that this other astrocyte remains in steady state; that is, its membrane potential, , and intracellular K⁺ and Na⁺ concentrations,  and , are constant. We assume that  = -90 mV,   = 135 mM and  = 12 mM.

As in (Ma et al., 2016; Huguet et al., 2016), we model I_gap using the Goldman-Hodgkin-Katz equation. That is, I_gap = I_Kgap + I_Nagap where

\(I_{Kgap}= P_{Kgap} F_{φA} \left(\frac{K_{iA} e^{(-φ_A )}-K_iA^0}{e^{-φ_A} -1} \right)\)  (8)

\(I_{Nagap}= P_{Nagap} Fφ_A \left( \frac{Na_{iA} e^{(-φ_A )}-Na_{iA}^0}{e^{-φ_A} -1} \right)\)

Here, \(\varphi{A} = (F/RT)(V_A-V_A^0)\). The constants P_Kgap and P_Nagap are the K⁺ and Na⁺ permeabilities, averaged over the entire cell membrane. Following (Ma et al., 2016), we assume that

P_Kgap = d_gap P_K         and          P_Nagap = 0.8 P_Kgap

where P_K = 6 *10⁻⁵ cm/s. We will vary d_gap, g^A_K and g_Kir in the analysis to determine how the dynamics depends on gap junction coupling strength and K⁺ currents.

Ion concentrations:  The neuron’s intracellular K⁺ and Na⁺ concentrations satisfy the equations

\(\frac{dK_i}{dt}=-\frac{10 S_N}{F Ω_N }(I_K-2I_{PN})\)   (9)

\(\frac{dNa_i}{dt}=-\frac{10 S_N}{F Ω_N }(I_{Na}-2I_{PN})\)

where S_N is the neuron’s surface area and W_N is the volume of the neuron’s cytoplasm. The factor ’10’ is needed for consistency of units.

The astrocyte’s intracellular K⁺ and Na⁺ concentrations satisfy the equations

\(\frac{dK_iA}{dt}=-\frac{10 S_A}{F Ω_A }(I_K^A+I_{Kir}+I_{Kgap}-2I_{PA})\)

\(\frac{dNa_iA}{dt}=-\frac{10 S_A}{F Ω_A }(I_{Na}^A+I_{Kir}+I_{Nagap}-2I_{PA})\)

where S_A is the astrocyte’s surface area and Ω_A is the volume of the astrocyte’s cytoplasm.

The extracellular K⁺ and Na⁺ ion concentrations satisfy the equations

\(\frac {dK_e}{dt}=\frac {10 S_N}{F Ω_N } (I_K-2I_PN )+\frac {10 S_A}{F Ω_A }(I_K^A+I_{Kir}+I_{Kgap}-2I_{PA})\)  (10)

\(\frac{dNa_e}{dt}=\frac{10 S_N}{F Ω_N} (I_{Na}+3I_PN )+\frac{10 S_A}{F Ω_A }(I_{Na}^A+I_{Nagap}+3I_PA)\)

where Ω_E is the volume of the extracellular space, which is assumed to be a fixed fraction of the neuron’s volume; that is, Ω_E = α₀ Ω_N. In the simulations, we let S_N= 10⁴ μm², Ω_N = 5 10³ μm³, S_A = 1.6 10³ μm², Ω_A = 2 10³ μm³ and α₀ = .3.

Network II

Network II consists of two mutually coupled neurons. Each neuron shares extracellular space with an astrocyte, which, as before, is electrically coupled with another astrocyte. Both ’units’, consisting of a neuron, astrocyte and shared extracellular space, are modeled precisely as Network I above, except we replace the Na⁺ and K⁺ leaks in (1) by a single leak current, I_L = g_L(V_N − E_L), where g_L = .02 and E_L = −60 mV. Moreover, we replace the excitatory current, I_exc, in (1) by a term corresponding to inhibitory synaptic input from the other neuron. That is, if j = 1 or 2, then we replace I_exc in the voltage equation for neuron j with

\(I_{syn}^j=g_{syn} s_k (V_N^j-E_{syn})\)

where \(k \neq j \) and s_k satisfies the equation 

\(s_k^,=α(1-s_k ) s_∞ (V_N^k )-βs_k\)

Here, E_syn = −85 mV is the synaptic reversal potential and s_∞ is defined as in (3). The parameter values for Network II are the same as Network I, except θ_n=−55, t₁ =2, φ=.2, g_syn=.05 and β=.18.

Results

Solutions of the two networks

Solutions of Network I are shown in Fig. 1. This figure demonstrates that whether the model can maintain repetitive spiking depends on several factors including the input frequency (f_r), the strengths of the Na⁺-K⁺ ATPase pumps (ρ_Nand ρ_A) and the strength of gap junction coupling (d_gap). Fig. 1A shows that the neuron can maintain a 30 hz firing rate for 5 seconds for moderate levels of gap junction coupling and Na⁺-K⁺ ATPase pump strengths. However, as shown in Fig. 1B, if the input rate is increased to 40 hz, then the neuron stops firing at around 3 seconds, at which time it goes into so-called depolarization block. If we remove gap junction coupling by setting d_gap = 0, then, as shown in Fig. 1C, the neuron cannot maintain periodic firing, even at a lower input rate of 10 hz. If we increase the Na⁺-K⁺ ATPase pump strength, then, as shown in Fig. 1D, the neuron is able to maintain periodic firing.

Figure 1: Solutions of Network I for different values of input frequency (fr), the strengths of the neuron’s Na+ -K+ ATPase pump (rN) and the strength of gap junction coupling (dgap). For each plot, rA = .5, g^A_K, b = 3 and gKir = 0. A) With gap junctions, the neuron can maintain firing for moderate pump strengths and input frequencies. B) Even with gap junctions, sufficiently high input rates lead to depolarization block. C) Without gap junctions, the neuron cannot maintain firing at 10 hz, unless, as shown in D), the pump strength is sufficiently high. 

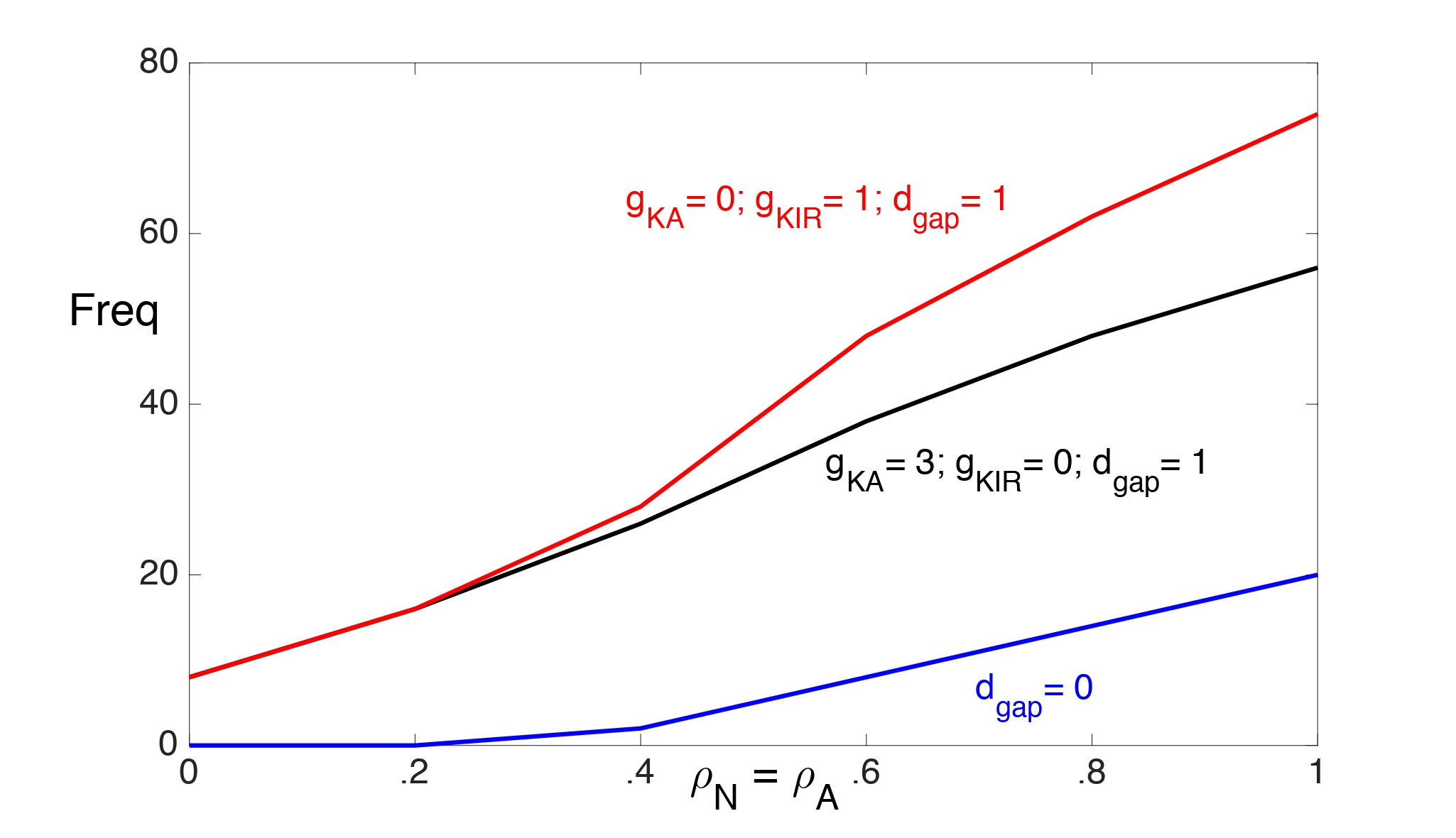
In Fig. 2 we illustrate the range of values of the Na⁺-K⁺ ATPase pump strengths (with ρ_N = ρ_A) and input frequencies for which the neuron is able to maintain spiking for 10 seconds. We consider the two cases: ( , g_Kir^A) = (3, 0) and ( , g_Kir) = (0, 1). We choose a smaller value for g_Kir to account for the K⁺ dependence of I_Kir  open probability. The neuron exhibits depolarization block for values of pump strengths and input frequencies above each curve.

Without gap junctions (d_gap = 0), there is almost no difference between these two cases in the frequencies at which the neuron can maintain steady spiking. In particular, without gap junctions, the inward rectifying K⁺ current does not seem to enhance K⁺ buffering, which is needed to prevent K_e from rising above the threshold for depolarization block.

Figure 2:  The range of values of the Na⁺-K⁺ ATPase pump strengths (with r_N = r_A) and input frequencies for which the neuron is able to maintain spiking for 10 seconds. The neuron exhibits depolarization block for values of pump strengths and input frequencies above each curve. The d_gap = 0 (blue) curve corresponds to both cases: ( , g_Kir) = (0,1) and ( , g_Kir)= (3,0).

With gap junctions (d_gap = 1), the neuron can maintain higher firing rates with just I_Kir  than with just  if the pump strengths are sufficiently strong. This is mainly because the threshold for K_e when the neuron exhibits depolarization block increases at higher pump strengths. (This will be demonstrated later.) Large K_e values strengthen I_Kir and enhance K⁺ buffering.

Fig. 3 shows solutions of Network II. With gap junction coupling (d_gap = 1), the network maintains anti-phase spiking. However, without gap junction coupling (d_gap = 0) the network switches from anti-phase to synchronous spiking at around 4.5 seconds. For this simulation, g_Kir = 1 and  = 0. The result is almost identical if instead, g^A_Kir = 0 and g^A_K = 3.

Figure 3:  Solutions of Network II. A) With gap junctions, the two neurons exhibit anti-phase oscillations. B) Without gap junction coupling, the network switches from anti-phase to synchronous spiking at around 4.5 seconds. C) With gap junctions, the model maintains a nearly constant K_e level, but not without gap junctions. D) Blow up of solution shown in B).

Isopotentiality and K⁺ buffering

Our results demonstrate that astrocytic gap junctional coupling plays a critical role in maintaining neuronal firing patterns. The basic mechanism underlying this behavior is so-called K⁺ spatial buffering: gap junction coupling allows astrocytes to maintain a nearly constant extracellular K⁺ concentration in the face of neuronal activity that would tend to increase it (Kofuji & Newman, 2004; Orkand et al., 2006). If the gap junction coupling strength is weak, then the astrocytes are not able to clear elevated extracellular K⁺ levels. This leads to increased neuronal excitability, which may change their firing properties. When extracellular K⁺ concentrations rise above some threshold, the neurons exhibit depolarization block.  

How does strong gap junction coupling lead to K⁺ spatial buffering? This depends on so-called isopotentiality; that is, an astrocyte’s associated syncytium provides powerful electrical coupling that equalizes the astrocyte’s membrane potential with its neighbors (Ma et al., 2016). To understand why isopotentiality leads to K⁺ spatial buffering, we first note that K⁺ currents are normally outward; that is, they allow for the flow of K⁺ ions from the cell’s inside to the extracellular space. In general, we can express a K⁺ current as I_K = g_K(V_A − ). If V_A >   , then I_K > 0 and the current is outward. In order for the K⁺ currents to be inward, the cell’s membrane potential must lie below the K⁺ reversal potential. When neurons spike, they release K⁺ into the extracellular space. Hence, K_e increases, as does    = (RT/F) ln(K_e/K_iA). However, because of isopotentiality, the astrocyte’s membrane potential remains nearly constant. This allows for V_A <    , so that the astrocyte’s K⁺ currents become inward and are, therefore, able to clear K⁺ from the extracellular space.

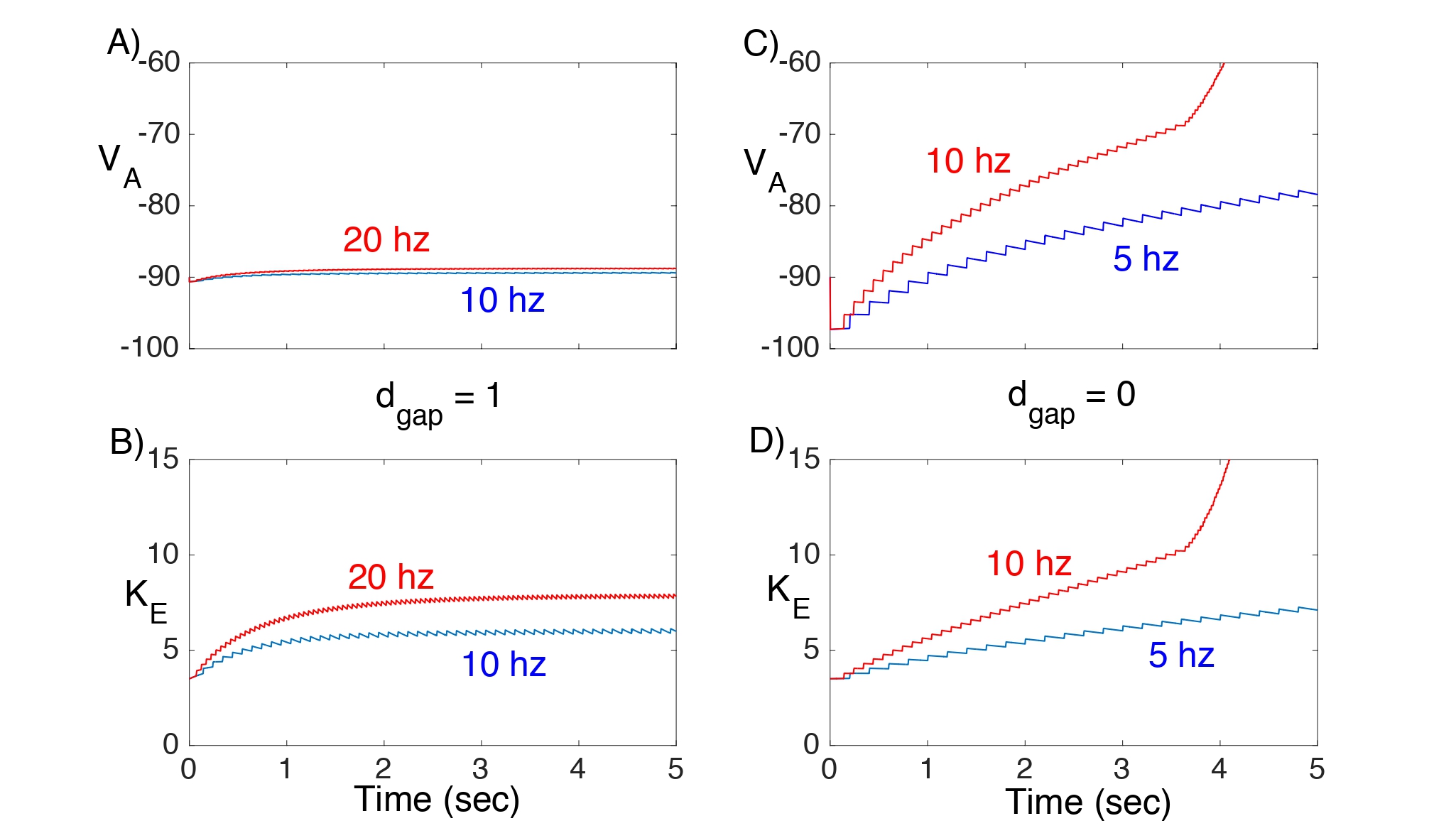
In Fig. 4, we consider Network I and plot the response of V_A and K_e to different excitatory input rates with (Fig. 4A,B) and without (Fig. 4C,D) gap junction coupling. When d_gap = 1, both the astrocyte’s membrane potential and extracellular K⁺ concentration remain nearly constant. However, when there are no gap junctions (d_gap = 0), there is a steady rise in both V_Aand K_e even at low input rates.

Figure 4:  Solutions of Network I showing V_A and K_e. Here, g_Kir = 3 and  = 0. A,B) With gap junctions the network can maintain nearly constant V_A and K_e , even at 20 hz input. C,D) This is not the case if there are no gap junctions.

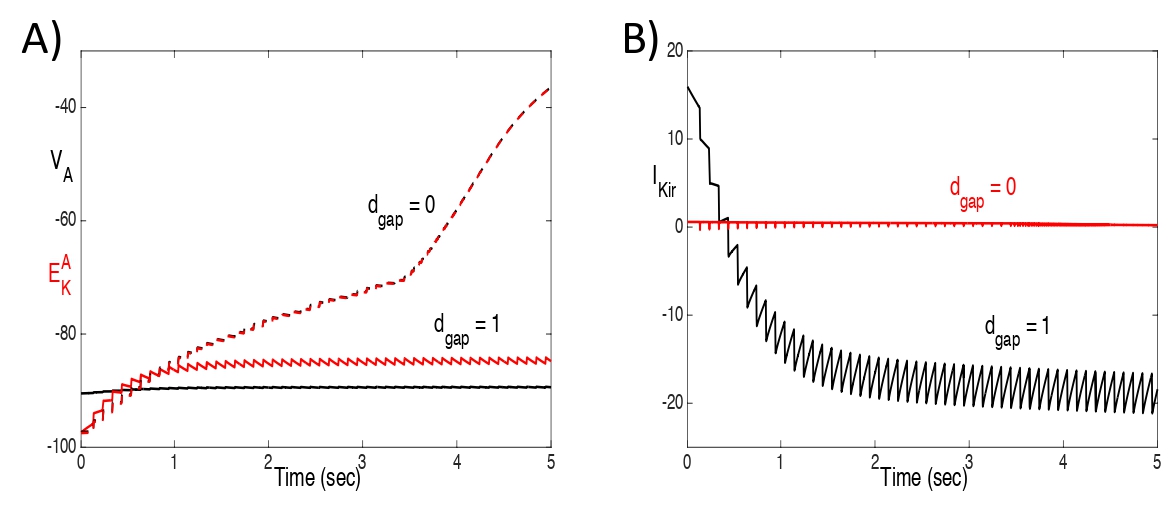
Fig. 5 shows plots of V_A ,  and I_Kir , with and without gap junctions, for the same solutions shown in Fig. 4 with an input rate of 10 hz. With gap junctions, V_A falls below    and I_Kir reverses (I_Kir< 0). Without gap junctions, V_A tracks very closely with    and I_Kirremains negligible.

Fig. 3C shows that for Network II, with strong gap junction coupling, K_e remains nearly constant; however, without gap junction coupling, there is a steady rise in K_e during neuronal firing.

Figure 5:  Plots of A) V_A and , and B) I_Kir, with and without gap junctions, for the same solutions shown in Fig. 4 with an input rate of 10 hz. With gap junctions, V_A falls below  and I_Kir reverses (I_Kir < 0). Without gap junctions, V_A tracks very closely with  and I_Kir remains negligible.

Analysis

 

We mathematically analyze Network I by first making some simplifying assumptions and then reducing the full model to a simpler set of equations. The analysis leads to a single equation for just K_e. This will be used to determine the K_e threshold for when the neuron exhibits depolarization block and help explain the response of the model to excitatory input.

We begin by noting that the total amounts of K⁺ and Na⁺ ions are conserved. That is 

\(Ω_e K_e+Ω_N K_i+Ω_A K_iA=K_{tot}\)  (11)

and

\(Ω_e {Na}_e+Ω_N Na_i+Ω_A Na_iA=Na_{tot}\)

are constant. We assume that

\(K_{tot}=Ω_e K_e^0+Ω_N K_i^0+Ω_A K_iA^0\)  and  \(Na_{tot}=Ω_e Na_e^0+Ω_N Na_i^0+Ω_A Na_iA^0\) 

where

\(K_e^0=4 \) mM, \(Na_e^0\) =135 mM,  \(K_i^0=K_iA^0=\)135 mM and  \(Na_i^0=Na_iA^0=\)12 mM.

We now make several assumptions in order to derive a reduced model. We first assume intracellular neuron electroneutrality; that is, K_i + Na_i =  +  is constant. Our next assumption is that the astrocyte’s intracellular K⁺ and Na⁺ concentrations are constant; that is,  and . With these assumptions we can solve for all of the ion concentrations in terms of K_e and the Network I model reduces to equations for just V_N , n, V_A and K_e.

We can reduce the model further using fast/slow analysis. The membrane potential V_A clearly evolves on a time-scale much faster than the ion concentration K_e. Since the astrocyte does not ’spike’, we may assume that V_A is close to steady state; that is, the right hand side of (6) is, to leading order, zero and we can solve for V_A in terms of the other variables. Note that if there is no I_Kir current (g_Kir = 0) then the right hand side of (6) is, in fact, a linear function of V_A. This is because if \(K_{iA}=K_{iA}^0\) and \(Na_{iA}=Na_{iA}^0\) , then the gap junction current can be written as

\(I_{gap}=g_{gap} (V_A-V_A^0)\)

where

\(g_{gap}=\frac{F^2}{RT} d_{gap} P_K (K_{iA}^0+.8Na_{iA}^0 ).\) (12)

Setting the right hand side of (6) equal to zero, we find that

\(V_A=\frac{g_K^A E_K^A+g_{Na}^A E_{Na}^A+I_{PA}-I_{exc}}{g_K^A+g_{Na}^A-g_{gap}}\)  (13)

The full Network I model is now reduced to equations for just V_N, n and K_e, which we write as

\(C_m \frac{dV_N}{dt}=-I_{Na}-I_K-I_{PN}-I_{exc}\)

\(\frac{dn}{dt}=\frac{ϕ(n_∞ (V_N )-n)}{τ_n (V_N )}\)

\(\frac{dK_e}{dt}=Φ(V_N,n,K_e )\)  (14)

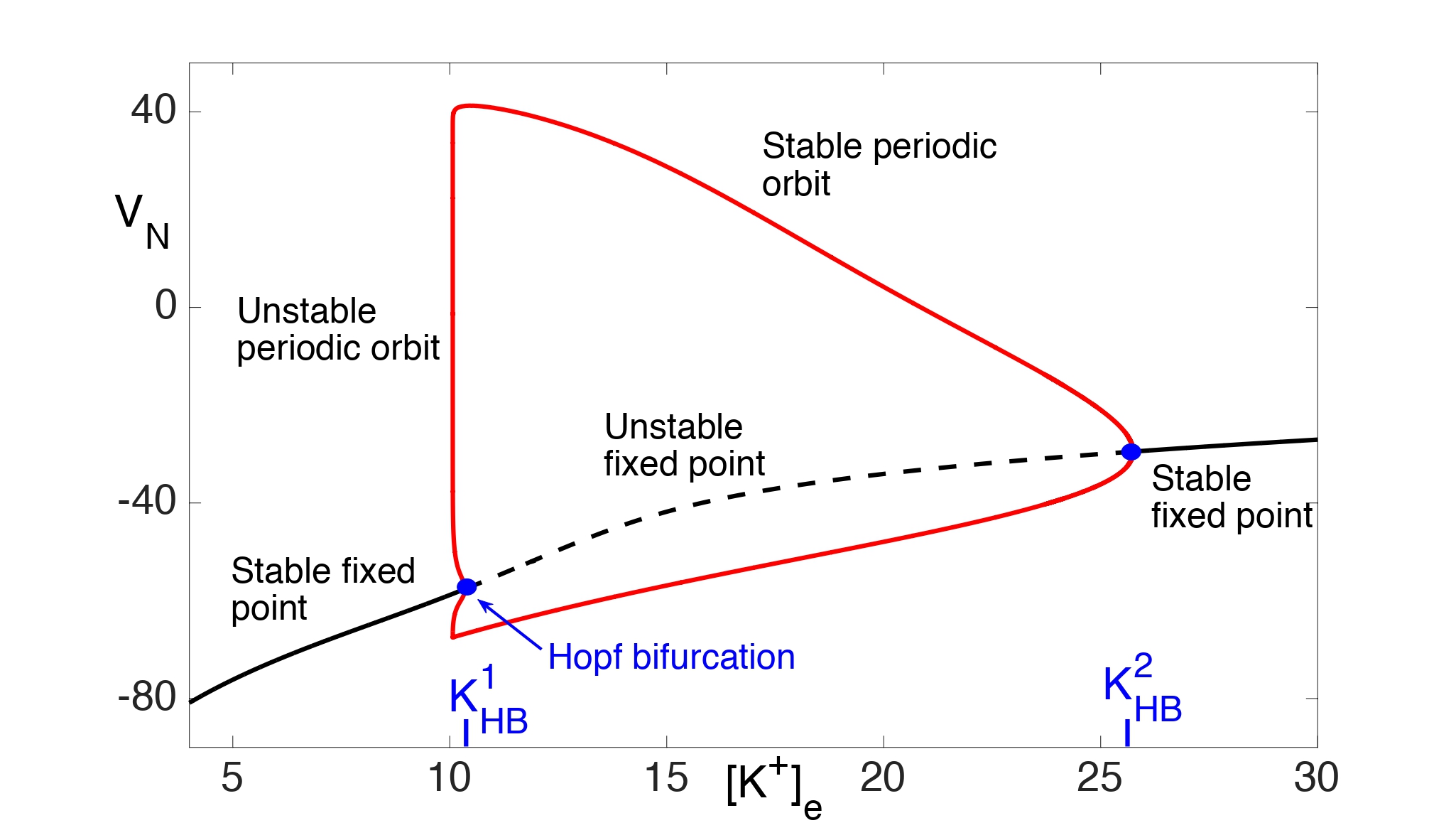
Assume, for now, that there is no excitatory input. Then fast/slow analysis is used to analyze the reduced system. If we consider the slow variable K_e to be a bifurcation parameter in the fast subsystem for (V_N, n), then the resulting bifurcation diagram is shown in Fig. 6. Note that there is a stable fixed point for \(K_e<K_HB^1≈10.35\) and \(K_e>K_{HB}^2≈25.75\). There is a subcritical Hopf bifurcation at  and a supercritical Hopf bifurcation at . Moreover, there are stable periodic orbits for  \(K_{HB}^1<K_e<K_{HB}^2.\)

We next consider the evolution of the slow variable K_e. This is done using the method of averaging. Denote the fixed points of the fast subsystem as (V_fp(K_e), n_fp(K_e)) and the stable periodic orbits as (V_P(t, K_e), n_P(t, K_e)). Let T(K_e) be the period of the periodic orbits. Near the branch of stable fixed points, K_e satisfies, to leading order,

\(\frac{dK_e}{dt}= Φ(V_{fp} (K_e ),n_{fp} (K_e ),K_e ) =Φ_{fp} (K_e )\)

Figure 6:  Bifurcation diagram for (14) with bifurcation parameter K_e. There are both supercritical and subcritical Hopf bifurcations and a branch of stable periodic orbits.

 

For \(K_{HB}^1<K_e<K_{HB}^2, K_e\) satisfies, to leading order,

\(\frac{dK_e}{dt} = \frac{1}{T(K_e)} ∫_0^{T(K_e)}Φ(V_P (t,K_e ),n_P (t,K_e ),K_e ) dt = Φ_{ave} (K_e )\)

We compute \(Φ_{fp} (K_e )\) and \(Φ_{ave} (K_e )\) numerically and the result is shown in Fig. 7A.

We first consider the K_e dynamics near the branch of stable fixed points of the fast subsystem with . Note that there exists K_P < K¹_HB such that \(Φ_{fp} (K_e )=0\) . Moreover, \( Φ_{fp} (K_e )>0\) for 0 < K_e < K_P and \(Φ_{fp} (K_e )<0\)for K_P < K_e < K¹_HB. This implies that K_e → K_P as t → ∞.

 

We next consider the spiking regime when . As shown in Fig. 7A, . Hence, K_e must increase and the neuron must approach depolarization block.

This analysis demonstrates that  is the threshold for when the neuron exhibits depolarization block. Fig. 7 shows that this threshold is an increasing function of the neuron’s Na⁺-K⁺ ATPase pump strength.

We next consider the neuron’s response to periodic excitatory input. Whenever the neuron spikes, there is also a spike in I_K. This leads to a fast rise in K_e. We now assume that at the spike times, K_eincreases by a fixed amount, which we denote as K_d. Based on numerics (see Fig. 4), we let K_d = .38 mM.

Figure 7:  A) Plots of Ф_fp(K_e) and Ф_ave(K_e). The threshold for depolarization block is K_e =K¹_HB . B) Plot of the depolarization block threshold versus the neuron pump strength r_N.

Between spike times, K_e satisfies (14), which depends on V_N  and n. We use fast/slow analysis to express these other variables in terms of K_e. This is done by first setting the right hand sides of (1) and (2) equal to zero and then solving for (V_N, n) in terms of K_e. However, the right hand side of (1) is a nonlinear function of V_N and n. In order to obtain an explicit formula for V_N, we note that between spikes, V_N is near a resting state and the channel activation terms, \(m_∞^3 (V_N) \) and n⁴, are very small. We, therefore, use the approximation 

I_Na  ≈  g_NaL(V_N − E_Na)    and    I_K  ≈  g_KL(V_N − E_K).                                         (15)

In this case, the right hand side of (1) is linear in V_N and does not depend on n. Setting the right hand side of (1) equal to zero, we find that

\(V_N=\frac{g_{NaL} E_{Na}+g_{KL} E_K-I_PN}{g_{NaL}+g_{KL} }\)  (16)

We can now express F in (14) as a function of just K_e; we denote this function as \(\psi(Ke)\). This is done by first replacing I_K by the approximation given in (15) and then using (16).

In summary, the reduced model is the following. Suppose that the excitatory input is at f_r hz. For each integer j and t_j = j · f_r /1000,

\(K_e (t_j^+ )=K_e (t_j^- )+K_δ\)

and

\(\frac{dK_e}{dt}=Ψ(K_e ) \)   for    t_j  <  t  <  t_j+1                     (17)

Solutions of this reduced model are shown in Fig. 8. With gap junctions (Fig. 8A) the neuron can maintain firing at 10 and 20 hz, since, in both cases, K_eremains below the threshold for depolarization block. Without gap junctions (Fig. 8B) the neuron cannot maintain firing at 10 hz if ρ_N = .5, since K_e increases past this threshold. However, increasing the neuron’s Na⁺-K⁺ ATPase pump strength to ρ_N = 1 allows the neuron to maintain a 10 hz firing rate.

Finally, we construct a 1-dimensional map; fixed points of the map correspond to the asymptotic behavior of K_e for the reduced model. To define the map, fix K₀ > 0 and let K_e(t; K₀) be the solution of (17) with K_e(0; K₀) = K₀. Then the map is defined as simply

\(Π(K_0 )=K_e (\frac{f_r}{1000};K_0 )+K_δ\)

Note that a fixed point of this map corresponds to a periodic solution of the reduced model (17).

In Fig. 8C,D we plot  P(K_e)−K_e  for the same parameter values used in Fig. 8A,B. Fixed points of P(K_e) correspond to zeros of the corresponding curves. Note in Fig. 8D that if d_gap =0 and ρ_N =.5, then P(K_e) > K_efor all values of K_e below the threshold for depolarization block. Hence, K_e must steadily increase past the threshold.

Figure 8:  A,B) Solutions of the reduced model (17). The dashed line corresponds to the threshold for depolarization block. C,D) Plots of the map P(K_e) − K_e. Fixed points P(K_e)  correspond to zeros of the corresponding curves.

 

Discussion

The main goals of this paper were to: 1) develop computational models to study mechanisms underlying astrocytes’ role in maintaining neuronal firing patterns; and 2) use mathematical tools to systematically reduce the complex model to a simpler system in order to characterize how solutions depend on network parameters and cellular processes. Simulations of the computational model demonstrate the importance of gap junctional coupling in K⁺ spatial buffering and, thereby preventing elevated levels of extracellular K⁺ leading to depolarization block. Using dynamical systems methods, we reduced the full Network I model to a one-dimensional map. Fixed points of the map determine whether the astrocyte can maintain extracellular K⁺ homeostasis so the neuron can faithfully respond to periodic input.

The basic mechanism for extracellular K⁺ clearance described in this study extends the concept of K⁺ spatial buffering, which was introduced more than a half century ago (Kofuji & Newman, 2004; Orkand et al., 1966). There have been several experimental, modeling, and analytic studies of K⁺ spatial buffering since then (Gardner-Medwin, 1983,Gardner-Medwin & Nicholson, 1983; Chen & Nicholson, 2000). However, the classic description does not take into account isopotentiality of the astrocyte syncytium. With sufficiently strong and widespread gap junction coupling, astrocytes near the region of elevated K⁺ concentration do not depolarize significantly and this provides a powerful driving force, , for K⁺ uptake through membrane K⁺ channels. This important role of syncytial isopotentiality was speculated in previous papers (Muller, 1996); however, this was not experimentally demonstrated until (Ma et al., 2016). As demonstrated in (Ma et al., 2016) syncytial isopotentiality minimizes the local high K_e-induced V_A depolarization, and this maintains a sustained driving force for K⁺ uptake. By extension, syncytial isopotentiality also increases the driving force for K⁺ release in distant regions where K_e remains at the physiological level. Additionally, increase in both driving forces creates a maximum driving force for intracellular K⁺ transfer from a high K⁺ region to remote regions with normal K⁺. Therefore, syncytial isopotentiality facilitates all three critical steps in K⁺ spatial buffering: K⁺ uptake, intercellular transfer and release (Kofuji & Newman, 2004). Furthermore, recent experiments demonstrate that syncytial isopotentiality arises in several regions throughout the central nervous system and may be a unified mechanism governing the operation of astrocyte networks (Kiyoshi et al., 2019; Kiyoshi & Zhou, 2019; Huang et al., 2018).

Some papers have proposed that the inward rectifying K⁺ current, I_Kir, is primarily responsible for K⁺ buffering. A computational model developed in (Sibille et al., 2015), for example, suggests that astrocytic Kir4.1 channels are sufficient to account for elevated extracellular K⁺ clearance, even without gap junctional coupling. However, there are important differences between the model presented in (Sibille et al., 2015) and that developed in this paper. In particular, the astrocyte membrane equation in (Sibille et al., 2015) contains a nonspecific leak current with a fixed reversal potential that helps stabilize the astrocyte membrane potential at -80 mV. This keeps the astrocyte’s membrane potential sufficiently hyperpolarized during neuronal activity so that I_Kir can reverse to an inward current. In our model, the astrocyte’s membrane potential remains hyperpolarized due to gap junctions and isopotentiality.

There have been numerous earlier papers that have addressed various issues related to modeling signals in astrocyte-neuronal networks. In particular, several papers have introduced models for spreading depolarizations, spreading depression, epilepsy, persistent activity and the propagation of Ca²⁺ waves (Cressman et al., 2009; Frohlich & Bazhenov, 2006; Hubel & Dahlemm 2014; Hubel et al., 2014; Huguet et al., 2016; Kager et al., 2002; O’Connell & Mori, 2016; Somjen et al., 2008; Ullah et al., 2009; Wei et al., 2014; Zandt et al., 2011). Moreover, several papers have used dynamical systems methods to reduce the complexity of the models and analyze how the neuronal spiking activity depends on the astrocytes’ ability to maintain ion homeostasis (Barreto & Cressman, 2011; Cressman et al., 2009; Frohlich & Bazhenov, 2006; Oyehaug et al., 2012; Zandt et al., 2011). Many of these previous models assumed that the role of the astrocytes is to simply buffer extracellular K⁺; this was modeled by including a simple buffering term in the equation for extracellular K⁺. We have built on and extended previous modeling studies by incorporating a detailed biophysical model for the astrocytes, considering the role played by gap junctions and reducing a model for the response of neurons to excitatory input to a one dimensional map.