Ulcerative colitis is a chronic inflammatory disease of the gastrointestinal system, affecting adults and children. Its cause is unknown, and the knowledge of reliable biomarkers is limited, especially for children. That makes the search for new biomarkers and pushing forth the analysis of the available data particularly challenging. We investigate proteomic data from children patients as a promising source, and tackle the problem implementing the recently developed parenclitic network approach to machine learning algorithms that solve classification task for proteomic data from healthy and diseased. We expect our approach to be applicable to other gastrointestinal diseases.
Introduction
Ulcerative colitis (UC) is a chronic relapsing non-specific disease, based on the inflammatory and destructive colonic mucosal lesions with the development of haemorrhages, erosions and ulcers, as well as extraintestinal manifestations of the disease and complications of local and systemic nature. This disease belongs to the immunoinflammatory pathology of unknown aetiology (Consensus for Managing Acute Severe Ulcerative Colitis in Children, 2011). On the average, the prevalence of UC varies from 30 to 240 per 100 000, while morbidity rate lies between 3 and 30 per 100 000 (С. Abraham & J.H. Cho, 2009).
In childhood and adolescence, the disease is diagnosed in about 15% to 40% of cases. Ulcerative colitis is one of those diseases, early detection of which often causes considerable difficulties for practitioners. In many cases, it takes a lot of time to make a diagnosis since the appearance of the first symptoms. Children may have atypical manifestations of endoscopic and morphological view, which makes it difficult to timely diagnosis. Identification of antinuclear antibodies (ANCA) in ulcerative colitis for adults has a high specificity (70%), nevertheless, for children, the value is a way below (Consensus for Managing Acute Severe Ulcerative Colitis in Children, 2011). These facts indicate the necessity to find new markers of disease with the help of which there will be an opportunity for earlier diagnosis of ulcerative colitis, and, hence, the well-timed appointment of suitable therapy (E.N. Fedulova et al., 2013).
Unfortunately, there is a relative lack of information about proven biomarkers in ulcerative colitis for children, despite the frequent use of biomarkers in clinical practice. Furthermore, those biomarkers, that have proved to be effective for adults, cannot be extrapolated to children without taking into account of the fact that the pathogenesis of many diseases is significantly different for children and adults (Viennois E. et al., 2015; Han N.Y. et al.; 2013, Hatsugai M. et al., 2010).
Inspired by the recent success of the combined graph and machine learning analysis for several kinds of spectral data, from metabolomics of nephritis and leukaemia to proteomics of cancer (M. Zanin et al. 2013a, M. Zanin et al. 2013b), we implement and validate a computational method for children UC mass-spectrometry (MS) data.
This paper reports the comparison of well-established machine learning methods as well as developing the new parenclitic approach and analysing UC data. Classifiers that we have built using topology indices (such as centrality scores and their variations) allow us to divide patients into two classes with high accuracy that is up to 85%. Furthermore, classical random forest demonstrates the best performance.
Methods
Patients. The analysis was performed with proteomics data from 56 children patients, diagnosed with ulcerative colitis, with an average age of 12.6 years, maximal age of 17 years and minimal age of 5. A control group included 42 reportedly healthy children, with an average age of 11.4 years, maximum age of 16 and minimal age of 6.
Data. Proteomics data were obtained from Nizhny Novgorod Federal Research Institute of Pediatric Gastroenterology. Patient's serum was prepared in a standard way. For subsequent mass-spectrometric research the samples were subjected to sample preparation - treatment with magnetic particles «ProfilingKit 100 MB-WCX» (BrukerDaltonic, Germany). Mass spectra were obtained on a MALDI-TOF mass spectrometer BrukerAutiflex (BrukerDaltonic, Germany). For the application of samples on mass spectrometric targets, the matrix based on α-cyano-4-hydroxycinnamic acid was used, which allowed us to select serum peptides and proteins in the sample within the molecular weight range from 0 to 10,000 Da. These results were obtained in a form of mass-sheets with indicating quantities of mass to charge (m/z) for each mass-peak, its area and intensity.
Spectrometry data are typically quite variable in positions of specific peaks, which does not allow to use those as features for machine learning algorithms. Usual pre-processing would require splitting the whole range into bins and counting the number of peaks within each one as derivative features (M. Zanin et al. 2013a). We had to resolve the issues of skewed density of peaks across the spectrum and the robustness of method for different number of bins. To overcome the former, we employed logarithmic binning (Fig.1), and to address the latter we varied the number of bins as N = {10, 15, 20, 25, 30, 35}. Pre-processing yields a table with the patient ID, case/control label and columns of bin counts as features. Thus, each patient received a set of N features after the completion of this procedure, hence, constructing a histogram. The number of bins can be changed.
Figure 1. MS-peak density distribution for the 36 patients with linear (left) and logarithmic scale binning (each patient indicated by a different colour).
Data Analysis and Machine-Learning Algorithms
Random Forest. This algorithm (Breiman L., 2001) is an extension of simple decision tree algorithm under which we construct multitude of decision trees. All trees are built independently according to the following scheme. Select subsample of training sample of size sample_size for building a tree (for each tree - its own subsample). To build each splitting in the tree one considers max_features of random features (for each new splitting — its own random features). Choose best attribute and its splitting (according to a predetermined criterion). The tree is constructed, as a rule, until exhaustion of the sample (while the leaves will not remain the representatives of only one class). Classification is performed by voting: each tree classifies the classified object to one of the classes and the winning class is the class for which voted for the greatest number of trees.
Logistic Regression. This is a method of constructing a linear classifier, allowing to estimate a posteriori probability of belonging of objects to classes. Logistic regression (Hastie, T. et al., 2009) and other classifiers use biomarkers as predictors. In the analysis of original data, they are number of values from mass spectrum fallen in specific bin (interval). Using parenclitic network analysis we transform source features into topological indices. The outcome is measured with a dichotomous variable in which there are only two possible outcomes - sick or healthy. Binarity of this variable arise from application of threshold which we can modify while also modifying the distribution of patients into classes.
Support Vector Machine (SVM). The algorithm also belongs to the family of linear classifiers as logistic regression. The main idea of linear SVM (Cortes C. & Vapnik V., 1995) is to build to build a hyperplane with the maximum width of strip separating two classes.
All the work has been done by using Python 3 programming language with scikit-learn, numpy and pandas packages. Moreover, in order to avoid overfitting, we have used 10-fold cross-validation. The best parameters of all standard algorithms are determined by GridSearchCV procedure from scikit-learn package. They cannot be revealed because of cross-validation technique that we used, which averages the results of multiple runs of the algorithm.
Parenclitic networks analysis. Beside producing features through simple bin counting, we make use of the recently introduced parenclitic network approach, which validity for spectral data has already been supported (M. Zanin et al. 2013a, M. Zanin et al. 2013b). It allows to build a network (a graph) for each patient denoting the original features as nodes, and connecting each pair by edges in case their values deviate abnormally from the control group statistics. The topological indices of the resulting network display hidden associations between the features and serve as secondary features for machine learning algorithms. Intuitively, healthy subjects should be associated with random-like networks, as the strongest links are expected to be the result of noise in the biological processes and in the measurement; on the other side, oncology subjects should present networks with non-trivial topologies. Here we outline the necessary steps in detail:
Building a network:
1. Select control group from healthy patients. Control group (20 patients) is a part of healthy patients that is chosen randomly to represent reference model.
2. Build linear regression model based on control group for each pair of markers, mi and mj:
mi=ai,j+bi,j*mj,
where ai,j and bi,j are regression coefficients.
3. Build complete weighted network for each patient, in which each node corresponds to a particular feature, and links are weighted according to
wi,j=|mi-(ai,j+bi,j*mj )|/σi,j ,
where σi,j is a standard deviation of errors in the linear regression model for a control group.
4. Delete links between certain nodes in accordance with the threshold. The best threshold is chosen after running classification algorithms and getting results. Initially, we obtain networks, graphs and new datasets for each threshold in [0.1, 7.0] with step is equal to 0.1.
Figure 2. Visual representation of parenclitic networks for arbitrary patients. Networks with green nodes represent healthy individuals, networks with the red nodes - patients with ulcerative colitis.
Describing network with topological indices.
1. Network for each patient is characterised by centrality scores (Albert R. & Barabasi A.L, 2002; Boccaletti. S et al., 2006; Freeman L., 1978/79): degree centrality, closeness centrality, betweenness centrality, eigenvector centrality, Katz centrality, edge betweenness centrality, current flow closeness centrality, current flow betweenness centrality, communicability centrality, load centrality. Each centrality is a measure of intrinsic properties of a graph. For example, degree centrality shows the number of ties that a node has. Closeness centrality calculated as the sum of the length of the shortest paths between the node and all other nodes in the graph. Betweenness centrality is equal to the number of shortest paths from all vertices to all others that pass through that node.
2. Formation of a new dataset. Each characteristic is a vector for which the average and maximum value are found. After this step, these values become our new features for the patient. Eventually, the number of topological indices is 20.
3. Applying machine learning techniques for classification on the new dataset. We use classical classification algorithms (random forest, SVM, logistic regression) on our new data where features are our topological indices and objects are patients.
To illustrate this approach let us consider a visual representation of some parenclitic networks for patients from the dataset with UC shown in Fig. 3.
This visualisation allows us to make sure that even visually patients can be divided into two classes, therefore classification algorithm will be able to do it by itself after describing these networks with topological indices. For example, in this case, even the average and maximum degree of a node (topological indices for degree centrality) is enough for carrying out the classification.
Discussion and Further Work
We explored the performance of classification for binning data against the choice of binning and the number of bins. We concluded that the best result was obtained for N = 35 bins and logarithmic bins, which allowed to remove skewness in MS-peak density distributions (Fig.1). For this choice of binning we compared performance of different classification algorithms to find consistently high accuracy (85-88%), specificity (73-83%) and sensitivity (89-95%), see Table 1.
Table 1. The classification results for UC dataset.
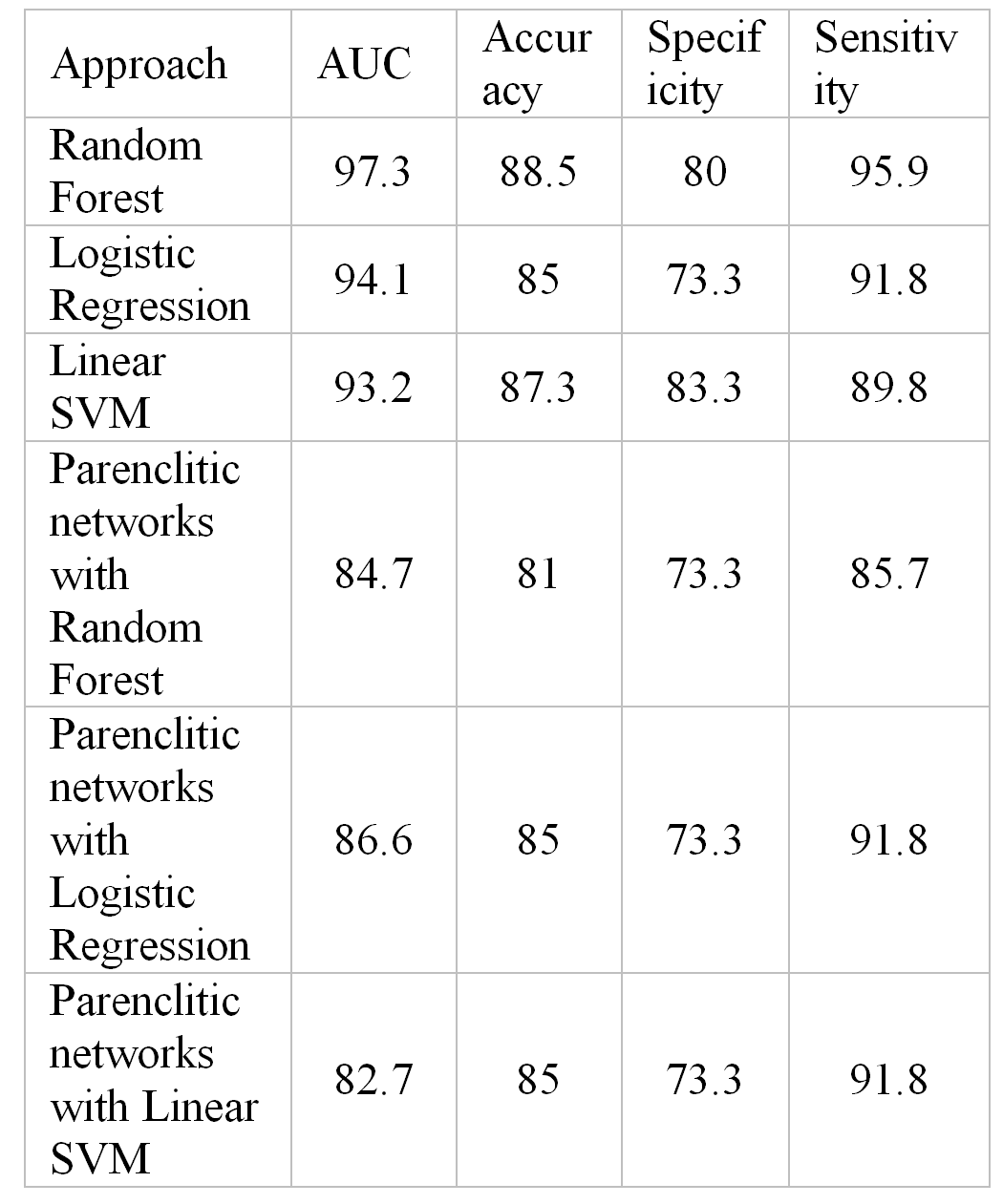
The performance of the parenclitic network approach compares well to the results for the primary features, based on binning (Table 1). Although it is more labour-intensive, it nevertheless has an additional degree of freedom for improving the quality of classification by using new distance metrics at the stage of preprocessing of data, keeping existing machine learning algorithms.
Another advantage of parenclictic networks is the potential of visual representation, where a graph can be plotted for each patient. Example cases shown in Figure 2 clearly demonstrate the difference between the healthy and diseased patients, the networks for the former being ill-centred and disjoint, while for the latter they typically display a few central nodes. Importantly, by construction, those central nodes correspond to the intervals in MS data, where consistently abnormal density is observed. It indicates the regions of interest, where peptide markers of UC must be sought.
The results summarized in Table 1 demonstrate that Random Forest algorithm shows the best performance with Accuracy 88.5% and AUC ~ 0.97. The method is quite simple, works fast and is the most appropriate for our analysis.
While the current study confirmed the applicability of machine learning approach to classify UC proteomic data, the directions for future work are clearly seen. First, there is a room for improving the measure for the distance between the object and the control group. Indeed, the linear regression model that minimises the regression residuals, may not work well when deviations are close to the corresponding line, or when regression is simply a poor approximation of the control group. Another improvement can be done by separating the test groups for cross-validation with the control group for the construction of the reference model, which, however, requires more extensive data. Ultimately, it is challenging to explore the potential for multi-class classification of MS data to distinguish between several different gastrointestinal diseases. The presented results already give a strong indication of the potential of the method and we expect their further validation towards the use as a complementary diagnostic method.
Author contributions
S.K., A.Z., M.I. and E.F. proposed and designed the study, S.K. performed data acquisition and initial analysis, M.I. and A.Z. contributed to the numerical method, A.R. performed numerical analysis, A.R., A.Z. E.F. and M.I. wrote the paper.
| Attachment | Size |
|---|---|
| 1.15 MB |
A.R., M.I. and A.Z. acknowledge Russian Ministry of Education and Science, agreement N 02.G25.31.0157 according to Russian Government Statement No. 218. Computations were carried out on the Lobachevsky University supercomputer.
Consensus for Managing Acute Severe Ulcerative Colitis in Children: A Systematic Review and Joint Statement From ECCO, ESPGHAN, and the Porto IBD Working Group of ESPGHAN (2011).
С. Abraham & J.H. Cho (2009). Inflammatory bowel disease. N. Engl. J. Med. Vol. 361, 2066-2078.
E.N. Fedulova, E.I. Shabunina, A.S. Gorodetsov, A.V. Lebedev (2013). A new approach to the differential diagnosis of Crohn's disease and ulcerative colitis in children. Herald of Northwestern State University № 1, 84-87.
Viennois E, Baker MT, Xiao B, Wang L, Laroui H, Merlin D (2015). Longitudinal study of circulating protein biomarkers in inflammatory bowel disease. J Proteomics.
Han NY, Choi W, Park JM, Kim EH, Lee H, Hahm KB (2013). Label-free quantification for discovering novel biomarkers in the diagnosis and assessment of disease activity in inflammatory bowel disease.
Hatsugai M, Kurokawa MS, Kouro T, Nagai K, Arito M, Masuko K, Suematsu N, Okamoto K, Itoh F, Kato T (2010). Protein profiles of peripheral blood mononuclear cells are useful for differential diagnosis of ulcerative colitis and Crohn's disease.
Breiman L (2001) Random Forests. Machine Learning 45: 5–32.
Cortes C & Vapnik V (1995). Support Vector Networks. Machine Learning 20: 273–297.
Hastie, T., Tibshirani, R., Friedman, J (2009). The Elements of Statistical Learning, 2nd edition. — Springer. — 533 p.
M. Zanin, D. Papo, J.L. Solís, J.C. Espinosa, C. Frausto-Reyes, P.P. Anda, Sevilla- R. Escoboza, R. Jaimes-Reategui, S. Boccaletti, E. Menasalvas, P. Sousa (2013a). Knowledge discovery in spectral data by means of complex networks. Metabolites. - Vol. 3(1). - P. 155-67.
M. Zanin, E. Menasalvas, S. Boccaletti, P. Sousa (2013b). Feature Selection in the Reconstruction of Complex Network Representations of Spectral Data. PLoS ONE 8(8): e72045. doi:10.1371/journal.pone.0072045.
Albert R. & Barabasi A.L. (2002). Statistical mechanics of complex networks. Reviews of Modern Physics. Vol.74, P.47.
Boccaletti. S, Latora V., Moreno Y., Chavez M., Hwang D.U. (2006). Complex Networks: Structure and Dynamics. Phys. Rep.; Vol. 424 P.175-308.
Freeman L. (1978/79). Centrality in social networks conceptual clarification. Social Networks. Vol. 1 P. 215-239.




