Opera Medica et Physiologica

Traveling Chimera Pattern in a Neuronal Network under Local Gap Junctional and Nonlocal Chemical Synaptic Interactions

Author Affiliations

Arindam Mishra1,2*, Suman Saha2, 3, Dibakar Ghosh5, Gregory V. Osipov6, Syamal K. Dana2,4 

1 Department of Physics, Jadavpur University, Jadavpur, Kolkata 700032, India;
2 Center for Complex System Research Kolkata, Kolkata 700094, India;
3 Department of Instrumentation and Electronics Engineering, Jadavpur University, Kolkata 700098, India;
4 CSIR-Indian Institute of Chemical Biology, Jadavpur, Kolkata 700032, India;
5 Physics and Applied Mathematics Unit, Indian Statistical Institute, Kolkata-700108, India;
6 Department of Control Theory, Nizhni Novgorod State University, Gagarin Avenue 23, 606950, Nizhni Novgorod, Russia.

Corresponding author: 

Arindam Mishra (arindammishra@gmail.com)

Syamal K. Dana (syamaldana@gmail.com)

Published ahead of print March 29, 2017; Printed March 31, 2017; OM&P 2017 Volume 3 Issue 1, pages 14-18; doi:10.20388/omp2017.001.0043

Keywords:

Abstract: 

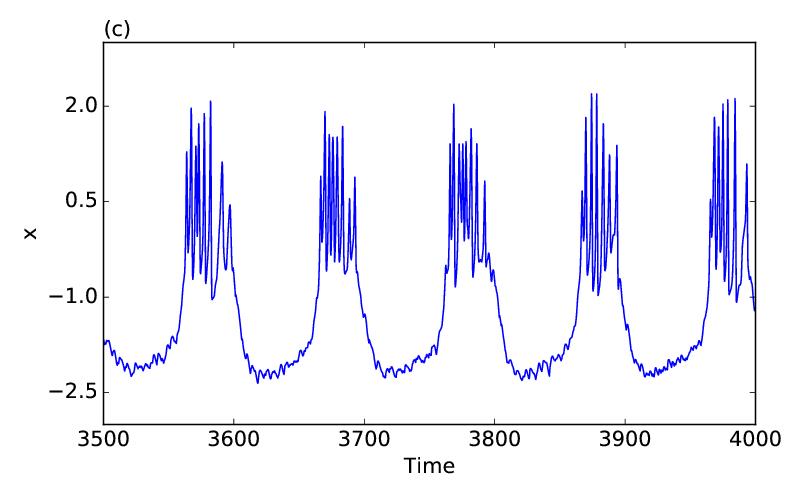
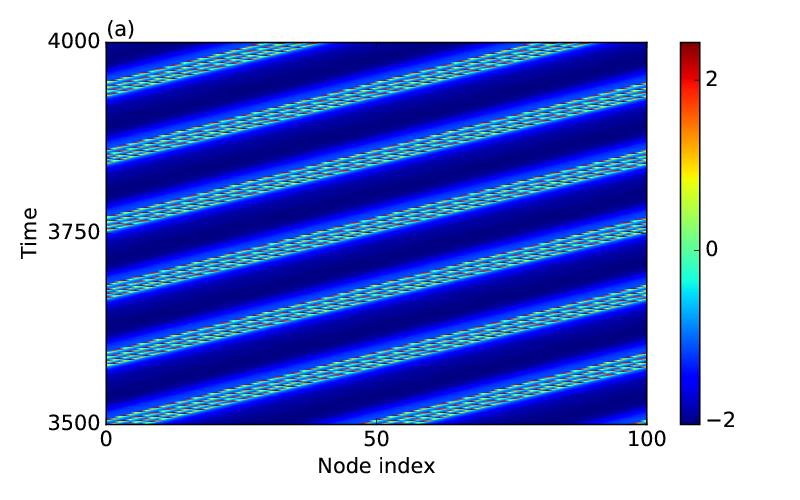
A spatially stable pattern of two coexisting coherent and incoherent subpopulations in nonlocally coupled dynamical systems is called as chimera states and seen in many paradigmatic limit cycle as well as chaotic models where the coupling interaction is basically diffusive type. In neuronal networks, besides diffusive electrotonic communication via gap junctions, chemical transmission occurs between the pre-synapse and post-synapse of neurons. We consider, in a numerical study, a network of neurons in a ring using the Hindmarsh-Rose (HR) bursting model for each node of the network and, apply attractive gap junctions for local coupling between the nearest neighbors and inhibitory nonlocal coupling via chemical synaptic transmission between the distant neighbors. For a range of gap junctional and chemical synaptic coupling strengths, a subpopulation of the neuronal network, in the ring, bursts asynchronously and another subpopulation remains silent in a synchronous state. The bursting subpopulation of neurons fires sequentially along the ring when the number of firing nodes remains same but change their positions periodically in time. It appears as a traveling chimera pattern in the ring when the dynamics of the individual bursting nodes is chaotic. The chimera pattern travels in a reverse direction for a larger chemical synaptic coupling strength. A purely inhibitory chemical synaptic coupling can produce a similar traveling chimera pattern, however, the dynamics of the firing nodes is then periodic.

 

Introduction
 
In the animal world, many mammals such as, dolphins, migratory birds, crocodiles, are found capable of sleeping with one eye open and another closed (Bressler and Kelso, 2001; Rattenborg et al., 1999). Thereby one half of their brain when resting, the other half is awake and alert at the same time. Such a state is called as unihemispheric sleep (Levy et al., 2000; Rattenborg et al., 2000; Mathews et al., 2006). EEG records on unihemispheric sleep experiments reveal that, in the sleeping hemisphere, neurons perform synchronous activity while, in the awake side, they are asynchronous. This natural activity in the brain of mammals is quite similar to the Kuramoto’s observation in 2002 that a network of identical oscillators symmetrically coupled via nonlocal coupling spontaneously breaks into coherent and incoherent subpopulations for stronger coupling and, they coexist with each other (Kuramoto and Battogtokh, 2002). The abundance of coexisting incongruous images in Greek mythology inspired Strogatz (Abrams and Strogatz, 2004; Abrams et al., 2008) to coin a name chimera states for such a coexisting coherent and incoherent spatial pattern in an ensemble of oscillators. Since then, it became an active area of research in non-linear dynamics. Chimera states were first observed in nonlocally coupled identical phase oscillators (Kuramoto and Battogtokh, 2002; Abrams and Strogatz, 2004; Martens et al., 2010) but later they were found in limit cycle (Sethia et al., 2013) and chaotic oscillators (Omelchenko et al., 2011; Gu et al., 2013; Schmidt and Krischer, 2015; Larger et al., 2013; Dudkowski et al., 2014) and most surprisingly, in globally coupled oscillators (Kaneko, 1990; Sethia and Sen, 2014; Yeldesbay et al., 2014; Hens et al., 2015; Mishra et al., 2015). Chimera states have been evidenced in laboratory experiments, chemical systems (Tinsley et al., 2012; Wickramasinghe and Kiss, 2013), optoelectronic systems (Hagerstrom et al., 2012), a network of metronomes (Martens et al., 2013). Recently, chimera states were explored numerically in practical systems, superconducting Josephson junction array (Lazarides et al., 2015; Mishra et al., 2017a,b) and neuronal network (Hizanidis et al., 2014; Bera et al., 2016b; Bera and Ghosh, 2016; Glaze et al., 2016; Majhi et al., 2016; Maksimenko et al., 2016).
A common feature of chimera pattern is that the size of the coexisting coherent and incoherent subpopulations remain same in time; they do not change their position and number in the subpopulations. In specific case studies of chimera states, a kind of metastability was reported (Mishra et al., 2015, 2017b) where the size of the incoherent subpopulation was seen changing in time. Such metastability is an important feature of neuronal network (Friston, 1997), which is yet to be given its due attention. By this time, a new kind of traveling chimera pattern was reported (Bera et al., 2016a), recently, in neuronal networks, where coexisting subpopulations in coherent and incoherent states change their positions in regular interval although the number of neurons in two subpopulations remain same. The dynamical nodes alternatively fires in a bursting state and a resting state periodically and the firing pattern moves sequentially along the ring. At any instant of time, the resting subpopulation remains synchronous while the bursting subpopulation becomes asynchronous.
A combination of excitatory and inhibitory local coupling via chemical synapses was used there in neuronal networks where the traveling chimera pattern (Bera et al., 2016a) was observed. Real neurons, on the other hand, interact via electrotonic gap junctions as well as chemical transmission between the pre-synaptic and the post-synaptic dendrites. Accordingly, in this paper, we consider both the gap junctional and the chemical synaptic interactions that are active in a ring of neurons. We keep in mind that a single neuron can only release one selective neurotransmitter, GABA receptor or Glutamate. GABA receptor plays inhibitory role while Glutamate sends excitatory signal to post-synapses. We assume that the gap junctions allow local communication between the nearest neighbors and the inhibitory chemical synaptic coupling builds nonlocal interactions between the distant neurons. We search for chimeralike patterns in such a network of neurons, however, observe a travelling chimera pattern instead. For a range of attractive gap junctional and inhibitory chemical synaptic coupling strength, the chimera pattern travels along the ring in one direction and, interestingly, reverses the direction of travel for stronger inhibitory chemical synaptic interaction. We find a similar traveling chimera pattern for purely inhibitory chemical synaptic coupling in the ring, however, the dynamics of the firing subpopulation is a periodic bursting instead of a chaotic bursting as seen for the combination of  coupling in the previous case. We mention that a sequential switching activity was reported earlier (Levanova et al., 2013; Mikhaylov et al., 2013) in 3-node network motifs using a type of inhibitory synaptic coupling, which we extended here for a larger network under inhibitory chemical synaptic as well as attractive gap junctional interactions. Instead of sequential switching of a single node, we report here a sequential firing of a bunch of nodes that mimics the traveling chimera pattern.
 
Network of Neurons
 
We build a ring of N identical nodes using the HR model for each node and apply two types of coupling interactions as described in Fig. 1. Each node is connected to its nearest neighbors by electrotonic gap junctions and to distantly neighboring nodes by nonlocal chemical synaptic coupling with a chosen coupling radius. Each node is represented by open circle; the local gap junctional links are represented by black lines while the non-local chemical synaptic links are shown for each node to all distant nodes by dashed lines (red lines). There is no chemical synaptic coupling between two immediate next neighbors on both sides of a node. Each node in the ring is connected in a similar manner to their neighbors and interacts in a similar fashion.
Figure 1. Schematic diagram of a neuronal network. Open circles represent HR neurons connected to their nearest neighbors by local gap junction links in black lines. Red dashed lines represent non-local chemical synaptic links shown for one node, which is true for all other nodes.
Figure 1. Schematic diagram of a neuronal network.  Open circles represent HR neurons connected to their nearest neighbors by local gap junction links in black lines. Red dashed lines represent non-local chemical synaptic links shown for one node, which is true for all other nodes.
 
The dynamics of i-th node of the ring is described by,
 
 
 
where i=1, 2, 3,..., N with boundary conditions, x0=xN and xN+1=x1, vsis the reversal potential, \(Γ(x_j )=\frac{1}{1+e^{-λ(x_j-Θ_s ) }}\) defines a chemical synaptic coupling function. k1 and k2 are strengths of gap junctional interaction and chemical synaptic coupling, respectively. P is the coupling radius that denotes the number of nodes on both sides of each node to which it communicates via chemical synaptic interactions (excluding two nearest neighbors). The coupling parameters for each node are chosen as Θs=-0.25,vs=2,λ=10,P=40 and all the nodes (N = 100) are identical. The system parameters are a = 1, b = 3, c = 1, d = 5, r = 0.01, s = 5 and xR=-1.6 when an uncoupled node exhibits periodic bursting as shown in Fig. 2.
Figure 2. Periodic bursting of an isolated HR model neuron. Parameters :a = 1, b = 3, c = 1, d = 5, r = 0.01, s = 5 and x_R=-1.6.
Figure 2. Periodic bursting of an isolated HR model neuron. Parameters :a = 1, b = 3, c = 1, d = 5, r = 0.01, s = 5 and xR=-1.6.
 
Results
 
We explore different emergent states in the ring network by varying the strengths of gap junctional and the chemical synaptic interactions. For a choice of k1=3 and k2=2, we find a traveling chimera pattern. Note that this is not limited to this particular set of coupling parameters rather true for a reasonably large range.
The spatiotemporal evolution of the x-variable of all the N=100 nodes in the network are shown in Fig. 3(a) which shows coexistence of two synchronous (blue) and asynchronous (cyan) subpopulations, however, they never remain stable in time but travels periodically from the bottom right corner to upper left corner. This type of moving coexisting pattern is defined here as a traveling chimera pattern, basically, traveling along the whole population periodically in time. The traveling nature of two coexisting states is further confirmed by snapshots of the xi-variable of all nodes at two different instants of time (black and red lines) in Fig. 3(b).
Figure 3. Traveling chimera pattern for k1=3 and k2=2. (a) Spatiotemporal pattern of the x-variable of all oscillators. The pattern travels from bottom right corner to upper left corner in time. (b) Snapshots of x-variable of all nodes at two different instants of time. Red line is for a later time than the black snapshot implying a traveling pattern from left to right.
Figure 3. Traveling chimera pattern for k1=3 and k2=2. (a) Spatiotemporal pattern of the x-variable of all oscillators. The pattern travels from bottom right corner to upper left corner in time. (b) Snapshots of x-variable of all nodes at two different instants of time. Red line is for a later time than the black snapshot implying a traveling pattern from left to right.
Figure 3. Traveling chimera pattern for k1=3 and k2=2.   (a) Spatiotemporal pattern of the x-variable of all oscillators. The pattern travels from bottom right corner to upper left corner in time. (b) Snapshots of x-variable of all nodes at two different instants of time. Red line is for a later time than the black snapshot implying a traveling pattern from left to right.
 
 
Each snapshot (black or red) shows that the whole population splits into coexisting coherent and incoherent sub-populations, however, their positions change in time as revealed by their shift in position when the plots are taken at two different instant of time. Two snapshots (black and red lines) show similar patterns, however, shifted in time.
Interestingly, if we increase the chemical synaptic coupling strength keeping the gap junctional strength constant, i.e., taking, k1=3 and k2=4, we find a similar kind of traveling chimera pattern, however, the traveling direction is reversed compared to the previous case. Figures 4(a) and 4(b) show a spatiotemporal evolution and snapshot of xi-variable, respectively, that clearly confirms the traveling nature of the chimera pattern. The pattern now travels from bottom left to right upper corner in the spatiotemporal plot as clearly seen from the spatiotemeporal plot in Fig. 4(a). Snapshots in Fig. 4(b) (red and black lines) confirm this reversal in the direction of movement. Figure 4(c) shows a time series of x that confirms chaotic bursting behavior of the nodes. A change of dynamics from periodic to chaotic bursting is reflected in the collective behavior of the chimera states. We explain this collective dynamics of the ring as an asynchronous firing of a subpopulation in a bursting state that moves sequentially along the ring periodically in time and this behavior coexists with another subpopulation in synchronous resting states that also changes periodically. Most importantly, the number of two coexisting subpopulations remains fixed for a fixed set of coupling parameters.
Figure 4. Traveling chimera for k1=3 and k2=4.(a) Spatiotemporal evolution of the x-variable shows the pattern is traveling from bottom left to upper right corner. (b) Snapshots of x-variable of all nodes at two different instants. (c) Time series shows a chaotic bursting behavior.
Figure 4. Traveling chimera for k1=3 and k2=4.(a) Spatiotemporal evolution of the x-variable shows the pattern is traveling from bottom left to upper right corner. (b) Snapshots of x-variable of all nodes at two different instants. (c) Time series shows a chaotic bursting behavior.
Figure 4. Traveling chimera for k1=3 and k2=4.(a) Spatiotemporal evolution of the x-variable shows the pattern is traveling from bottom left to upper right corner. (b) Snapshots of x-variable of all nodes at two different instants. (c) Time series shows a chaotic bursting behavior.
Figure 4. Traveling chimera for k1=3 and k2=4.(a) Spatiotemporal evolution of the x-variable shows the pattern is traveling from bottom left to upper right corner. (b) Snapshots of x-variable of all nodes at two different instants. (c) Time series shows a chaotic bursting behavior.
 
 
An interplay of diffusive gap junctional and chemical synaptic coupling creates the traveling chimera pattern and a change of traveling direction occurs with varying chemical synaptic coupling strength. We have checked that if the chemical synaptic coupling strength is less than or equal to the gap junctional coupling strength the direction of the chimera pattern travels in one direction and it reverses its direction when the chemical synaptic coupling strength is greater than the gap junctional coupling strength.
We find that a purely gap junctional coupling cannot produce the traveling chimera pattern. However, for a purely chemical synaptic coupling, a similar kind of traveling chimera pattern is seen for a relatively larger coupling strength k2=9. A spatiotemporal plot in Fig. 5(a) of xi-variable of all the nodes confirms this traveling character of the chimera states. Figure 5(b) represents the time series of xi-variable exhibiting periodic bursting behavior instead of a chaotic bursting.
Figure 5. Traveling chimera pattern for purely inhibitory synaptic coupling, k1=0,k2=9. (a) Spatiotemporal plot shows the traveling chimera pattern, (b) time series of xi of a bursting node exhibits periodic behavior.
Figure 5. Traveling chimera pattern for purely inhibitory synaptic coupling, k1=0,k2=9. (a) Spatiotemporal plot shows the traveling chimera pattern, (b) time series of xi of a bursting node exhibits periodic behavior.
Figure 5. Traveling chimera pattern for purely inhibitory synaptic coupling, k1=0,k2=9. (a) Spatiotemporal plot shows the traveling chimera pattern, (b) time series of xi of a bursting node exhibits periodic behavior.
 
 
Conclusion
 
We investigated a network of identical HR oscillators in a ring with local gap junctional interactions between the nearest neighbors and non-local chemical synaptic interactions between the distant neighbors. We observed a type of traveling chimera pattern for a choice of gap junctional and chemical synaptic coupling strengths. In such a state, a subpopulation of neurons fired asynchronously in a bursting state while another subpopulation remained synchronous in a silent state. The number of synchronous and asynchronous subpopulations did not change with time but their spatial position changed periodically which we called as a traveling chimera pattern. A subpopulation of neurons fired sequentially in a cyclic order along the whole population while others remained silent. The firing neurons showed chaotic nature of bursting. Most importantly, the size of the sequentially firing subpopulation remained same for a set of coupling parameters but could be changed by varying them. Very interestingly, by modulating the chemical synaptic coupling strength, a change of direction in the traveling chimera pattern was obtained. We searched for a simpler coupling if a purely gap junctional or chemical synaptic coupling could induce such a traveling pattern. We were unsuccessful so far with purely gap junctional coupling, however, a purely chemical synaptic coupling brought back the traveling chimera pattern for a relatively higher coupling strength. In this case the firing neurons exhibited periodic bursting behavior.
AttachmentSize
OMP_2017_001_0043.pdf1.12 MB
Acknowledgments: 

A.M is supported by the University Grants Commission, India. A.M. and S.S also acknowledge local support and hospitality for two week’s visit by the Lobachevsky state University of Nizhny Novgorod, Russia. D.G. and S.K.D. are supported by the SERB-DST (Department of Science and Technology), Government of India (Project No. INT/RUS/RFBR/P-181), GO acknowledges support of Russian Science Foundation (Project N 17-12-01534).

References: 

Abrams, D. M., Mirollo, R., Strogatz, S. H., and Wiley, D. A. (2008). Solvable model for chimera states of coupled oscillators. Phys. Rev. Lett., 101:084103.
Abrams, D. M. and Strogatz, S. H. (2004). Chimera states for coupled oscillators. Phys. Rev. Lett., 93:174102.
Bera, B. K. and Ghosh, D. (2016). Chimera states in purely local delay-coupled oscillators. Phys. Rev. E, 93:052223.
Bera, B. K., Ghosh, D., and Banerjee, T. (2016a). Imperfect traveling chimera states induced by local synaptic gradient coupling. Phys. Rev. E, 94:012215.
Bera, B. K., Ghosh, D., and Lakshmanan, M. (2016b). Chimera states in bursting neurons. Phys. Rev. E, 93:012205.
Bressler, S. L. and Kelso, J. (2001). Cortical coordination dynamics and cognition. Trends in Cognitive Sciences, 5(1):26 – 36.
Dudkowski, D., Maistrenko, Y., and Kapitaniak, T. (2014). Different types of chimera states: An interplay between spatial and dynamical chaos. Phys. Rev. E, 90:032920.
Friston, K. J. (1997). Transients, metastability, and neu-ronal dynamics. NeuroImage, 5(2):164 – 171.
Glaze, T. A., Lewis, S., and Bahar, S. (2016). Chimera states in a hodgkin-huxley model of thermally sensitive neurons. Chaos: An Interdisciplinary Journal of Nonlinear Science, 26(8):083119.
Gu, C., St-Yves, G., and Davidsen, J. (2013). Spiral wave chimeras in complex oscillatory and chaotic systems. Phys. Rev. Lett., 111:134101. 
Hagerstrom, A. M., Murphy, T. E., Roy, R., Hovel, P., Omelchenko, I., and Scholl, E. (2012). Experimental observation of chimeras in coupled-map lattices. Nature Physics, 8:658.
Hens, C. R., Mishra, A., Roy, P. K., Sen, A., and Dana, S. K. (2015). Chimera states in a population of identical oscillators under planar cross-coupling. Pramana – Journal of Physics, 84:229.
Hizanidis, J., Kanas, V. G., Bezerianos, A., and Bountis, T. (2014). Chimera states in networks of nonlocally coupled hindmarsh–rose neuron mod-els. International Journal of Bifurcation and Chaos, 24(03):1450030.
Kaneko, K. (1990). Clustering, coding, switching, hi-erarchical ordering, and control in a network of chaotic elements. Physica D: Nonlinear Phenomena, 41(2):137 – 172.
Kuramoto, Y. and Battogtokh, D. (2002). Coexistence of coherence and incoherence in nonlocally coupled phase oscillators. Nonlinear Phenomena in Complex Systems, 5:380–385.
Larger, L., Penkovsky, B., and Maistrenko, Y. (2013). Virtual chimera states for delayed-feedback systems. Phys. Rev. Lett., 111:054103.
Lazarides, N., Neofotistos, G., and Tsironis, G. P. (2015). Chimeras in squid metamaterials. Phys. Rev. B, 91:054303.
Levanova, T. A., Komarov, M. A., and Osipov, G. V. (2013). Sequential activity and multistability in an ensemble of coupled van der pol oscillators. The Eu-ropean Physical Journal Special Topics, 222(10):2417– 2428.
Levy, R., Hutchison, W. D., Lozano, A. M., and Dostro-vsky, J. O. (2000). High-frequency synchronization of neuronal activity in the subthalamic nucleus of parkinsonian patients with limb tremor. Journal of Neuroscience, 20(20):7766–7775.
Majhi, S., Perc, M., and Ghosh, D. (2016). Chimera states in uncoupled neurons induced by a multi-layer structure. Scientific Reports, 6:39033.
Maksimenko, V. A., Makarov, V. V., Bera, B. K., Ghosh, D., Dana, S. K., Goremyko, M. V., Frolov, N. S., Ko-ronovskii, A. A., and Hramov, A. E. (2016). Excitation and suppression of chimera states by multiplexing. Phys. Rev. E, 94:052205.
Martens, E. A., Laing, C. R., and Strogatz, S. H. (2010). Solvable model of spiral wave chimeras. Phys. Rev. Lett., 104:044101.
Martens, E. A., Thutupalli, S., Fourriere,` A., and Hal-latschek, O. (2013). Chimera states in mechanical oscillator networks. Proceedings of the National Academy of Sciences, 110(26):10563–10567.
Mathews, C. G., Lesku, J. A., Lima, S. L., and Am-laner, C. J. (2006). Asynchronous eye closure as an anti-predator behavior in the western fence lizard (sceloporusoccidentalis). Ethology, 112(3):286–292.
Mikhaylov, A. O., Komarov, M. A., Levanova, T. A., and Osipov, G. V. (2013). Sequential switching activity in ensembles of inhibitory coupled oscillators. EPL (Europhysics Letters), 101(2):20009.
Mishra, A., Hens, C., Bose, M., Roy, P. K., and Dana, S. K. (2015). Chimeralike states in a network of oscillators under attractive and repulsive global coupling. Phys. Rev. E, 92:062920.
Mishra, A., Saha, S., Hens, C., Roy, P. K., Bose, M., Louodop, P., Cerdeira, H. A., and Dana, S. K. (2017a). Coherent libration to coherent rotational dynamics via chimeralike states and clustering in a josephson junction array. Phys. Rev. E, 95:010201.
Mishra, A., Saha, S., Roy, P. K., Kapitaniak, T., and Dana, S. K. (2017b). Multicluster oscillation death and chimeralike states in globally coupled joseph-son junctions. Chaos: An Interdisciplinary Journal of Nonlinear Science, 27(2):023110.
Omelchenko, I., Maistrenko, Y., Hovel,¨ P., and Scholl,¨ E. (2011). Loss of coherence in dynamical networks: Spatial chaos and chimera states. Phys. Rev. Lett., 106:234102.
Rattenborg, N. C., Amlaner, C. J., and Lima, S. L. (2000). Behavioral, neurophysiological and evolu-tionary perspectives on unihemispheric sleep. Neuroscience &Biobehavioral Reviews, 24(8):817 – 842.
Rattenborg, N. C., Lima, S. L., and Amlaner, C. J. (1999). Half-awake to the risk of predation. Nature, 397:397–398.
Schmidt, L. and Krischer, K. (2015). Clustering as a prerequisite for chimera states in globally coupled systems. Phys. Rev. Lett., 114:034101.
Wickramasinghe, M. and Kiss, I. Z. (2013). Spatially organized dynamical states in chemical oscillator networks: Synchronization, dynamical differentiation, and chimera patterns. PLOS ONE, 8(11).
Yeldesbay, A., Pikovsky, A., and Rosenblum, M. (2014). Chimeralike states in an ensemble of globally coupled oscillators. Phys. Rev. Lett., 112:144103.

 

Copyright © 2014-2021 by Lobachevsky State University of Nizhny Novgorod. Privacy Policy | Terms of Service