The role of chaos in biological information processing has been established as an important breakthrough of nonlinear dynamics, after the early pioneering work of J.S. Nicolis and notably in neuroscience by the work of Walter J. Freeman and co-workers spanning more than three decades. In this work we revisit the subject and we further focus on novel results that reveal its underlying logical structure when faced with the cognition of ambiguous stimuli. We demonstrate, by utilizing a minimal model for apprehension and judgement related to Bayesian updating, that the fundamental characteristics of a biological processor obey in this case an extended, non-Boolean, logic which is characterized as a quantum logic. And we realize that in its essence the role of chaos in biological information processing accounts for, and is fully compatible with, the logic of “quantum cognition” in psychology and neuroscience.
Introduction: Chaos and Biological Information.
Dynamical systems as mathematical models, have always been used as one of the primary tools for understanding and predicting biological behaviour. This understanding, traditionally, was based on classical physics although recently quantum-physical considerations are also coming into play. With the advent of nonlinear chaotic dynamics the very notion that determinism implies predictability has been shattered and the role of the existing causal relations became less evident concerning the forecasting power for complex nonlinear dynamical systems. Although J.C. Maxwell and H. Poincaré were the first to postulate on the inherent predictive limitations due to the sensitive dependence on initial conditions exhibited by chaotic systems, it took almost a century for this idea to find roots in the mind of the scientific community at large. Now, we realize that predictions for nonlinear, complex systems can only be discussed in terms of a probabilistic framework, like in weather forecasting to mention an everyday example of complexity, and causality can be inferred by available, necessarily incomplete, information [Nicolis G. & Nicolis C., 2012; Basios & MacKernann, 2011].
Dynamical systems are described by their phase -or state- space, a space where their main variables define and live in. A trajectory in the phase space describes the dynamics and temporal evolution of the system. An attractor is a region in phase space where all, i.e. ‘almost all’ in mathematical terms, trajectories will eventually reside. Each attractor is characterized of it’s stability properties, and its dimensionality as well as its statistical and probabilistic, or measure-theoretic, aspects [Nicolis G. & Nicolis C., 2012]. We have all kinds of attractors, stable, unstable, metastable and for higher than two dimensional phase spaces of chaotic dynamics the so called ‘strange attractors’ came to be known. Strange indeed as they possess coexisting stable and unstable directions at once. This makes them take the form of a ‘fractal’, a geometrical object with a ‘fractal dimension’ living in the in-between of two integer dimensions. Each attractor, strange or not, has a basin of attraction where once inside it the system will eventually settle on the attractor. In the case of co-existing attractors the boundaries between them, most often than not, are fractals too.
An important measure associated with an (strange) attractor’s (fractal) dimension is its information carrying capacity. Information, quantifying the element of surprise, serves as a degree of the attractors’ irregularity. The realization of attractors serving as information rich carriers and their potential as information processors has been championed by J. S. Nicolis and A. Shaw since the late ‘70s and early 80’s [Nicolis G. & Basios 2015; West 2013; Nicolis J.S. et al 1986; Nicolis J.S. et al 1983; Shaw, 1981].
On elucidating the key role of the concept of information in biology, on the other hand, much has been achieved after the seminal question posed by E. Schroedinger “What is Life?” in his famous book which bears the same title. The idea of living entities as lowering entropy structures “machines producing negentropy and order” was further aided by the classic work of C. Shannon on information transmission.
Within these conceptual frameworks the junction of information, biology and dynamics was again ingeniously proposed by J.S. Nicolis [Nicolis, J.S. 1991; Nicolis G. & Basios, 2015]. He studied the role of chaos and noise in the dynamics of hierarchical systems by extending the work of C. Shannon. He incorporated dynamical notions in the study of information flow in biological information processors. This proposal of his created a lot of interest, at the time, albeit shadowed by the rapid development of the field. The pioneer neurophysiologist W.J. Freeman picked up the idea of J.S. Nicolis and identified the role of chaos in olfactory perception and the study of EEG (Electro-Encephalo-Gram) in a more general setting [W. J. Freeman, (2015); Freeman, 2013; Freeman et al., 2012; Freeman, 2001; Freeman, 2000]. Agnes Babloyanz, was also one of the first if not the first, that applied the techniques of attractor reconstruction from EEGs time series and pointed the signature of chaos and its role in brain dynamics [Babloyanz,1986]. After that an avalanche of papers proposed and established more and more sophisticated tools stemming from nonlinear dynamics and by now this kind of investigation is a standard procedure. The role of chaos and fractals in structure, function and dynamics concerning biological tissues and organs took root form then on. We know have diagnostic tools (notably for the heart and brain) based on these concepts.
While these developments were taking place describing the phenomenological large scale level of the dynamics of biological information, on the other end microscopic models where proposed for neuronal systems. These models started from very elementary “integrate and fire” models with linear components and the more realistic they grew the more nonlinearities were incorporated; with the inevitable appearance of chaotic behaviours. A detail enumeration of these models in the field of computational neuroscience can be found, for example in [Izhikevich, 2004].
Interestingly this cross-fertilization between cognitive and computational neuroscience from the one side and dynamical system theory and chaos from the other, led not only to breakthroughs in how we think about biological information processing but also to novel theoretical advances in dynamics. Among the most outstanding theoretical development was the discovery of the so called “blue sky catastrophe” a new type of bifurcation that would have passed undetected if it was not for the investigations of the underlying dynamics of neuron spike-train bursting brought forth by the work of A. Shilnikov, D. Turaev and co-workers [Shilnikov & Turaev, 2007; Shilnikov & Cymbalyuk, 2005; Wojcik et al (2011)].
Moreover the importance of nonlinear systems in understanding complex behaviour of biological rhythms has been recently advanced by an important conceptual and readily applicable breakthrough [Wojcik et al, 2014] that straddles the gab between nonlinear systems’ modelling and data analysis/treatment. By studying qualitative changes in the structure of corresponding Poincare-type return maps, the authors of [Wojcik al (2014)] provide a systematic basis for understanding plausible biophysical mechanisms for the regulation of rhythmic patterns generated by various “central pattern generations” (CPG or “pacemakers”). They demonstrate this in the context of motor control (gait-switching in locomotion) and in addition their analysis is also very relevant beyond motor control. Their technique [Wojcik al, 2014] can easily be applied, also, to the case of information processing; and it might provide further understanding for the pacemakers’ role and their “time-division-multiplexing-basis”, that we will encounter in Sect. 2.1, in relation to “chaotic itinerancy” (see also Fig. 2).
And last but not least we have the phenomena of stochastic and chaotic resonance in neural networks in the brain [McDonnel & Stocks, 2009; Mori & Kai, 2002] and the immense work by H. Haken and his collaborators [Haken, 1996; Haken, 2008] on self-organization and perception in brain dynamics that also cross-fertilize both fields of neuroscience and nonlinear dynamics.
Presently, modern concepts and tools from complexity help in bridging the gap between macroscopic and macroscopic mathematical modelling of biological processes. More specifically in the area of brain sciences, there is recently an intense activity and fast progress concerning mesoscopic models based on hierarchical networks, i.e clusters of neurons, extended neuronal networks and/or groups of neurons , “networks of networks” as they are often called. Novel structures and concepts such as “chimeras” appear in order to describe their complex dynamics. Dynamics that exhibit coexisting regimes of chaos and order, multiscale dynamics and cascades of bifurcations. Among the plethora of publications on the subject we refer to two recent ones [Hizanidis, et al 2016; Meunier et al, 2010] which provide key references therein
As we have seen the role of chaos in biological information processing has been established as an important breakthrough of nonlinear dynamics, notably in neuroscience, spanning more than three decades. Subsequently, in this work we review and report novel results that reveal its underlying logical structure. For our demonstration we use a minimal model for apprehension and judgement inspired from this breakthrough that we have related it to Bayesian updating. This brings forth the realization that a biological processor obeys essentially an extended, non-Boolean, logic fully compatible with, the so called, “quantum-logic”.
Metastable Chaos and Coexisting Attractors: revealing ambiguities
Let us now revisit the subject of biological information processing and chaos by briefly considering its main ingredients and its fundamental aspects. Because in this work our focus is to illustrate the underlying logical structure using a model with the minimum essential considerations in an as much as possible generic setting. The construction presented here follows previous work of ours outlined in [Gunji et al 2016; Gunji et al 2017]. We start with the fact that any act of information processing in an organism involves two separate phases (Fig.1):
(a) An expanding, exploratory, phase where the biological processor probes its environment and information from the outer world manifests via a set of impinging stimuli to its sensory channels. This phase involves motor-sensory coordination. During this phase the dynamics of the whole process expand in the available phase space i.e. the sum of its Lyapunov exponents is strictly positive. The pre-existing or newly formed attractors therefore must be strange-chaotic attractors able to accommodate information.
(b) A contracting, recollecting phase where the biological processor compresses information by contracting the basin of attraction toward one of the coexisting attractors. The raw stimuli thus are collected and represented in various pre-existing or newly formed categories. So the dynamics at this phase have to exhibit a strictly negative sum of Lyapunov exponents.
In deed, the compression in phase (b) results to ‘categorization’ and is characterized by a loss of information of the order of log(N/D) bits, where N is the dimension of the phase space and D the correlation dimension of the specific attractor that represents the category which carries and/or stores the information coming from the stimulus-signal. It is worth mentioning that the two phases can either executed in succession and/or in parallel. In any way this recurrent activity via a nonlinear feed-back loop guarantees that observation and categorization occur in unison, Fig. 1, [Nicolis J.S., 1991; Nicolis J.S., 1986; Tsuda & Fujii., 2004, Tsuda 2015].
Figure 1. The Two Phases of Biological Processing: Biological processors observe, and collect information, by probing their environment and comprehend it, by categorizing it.
Coexisting Attractors and fractal basin boundaries
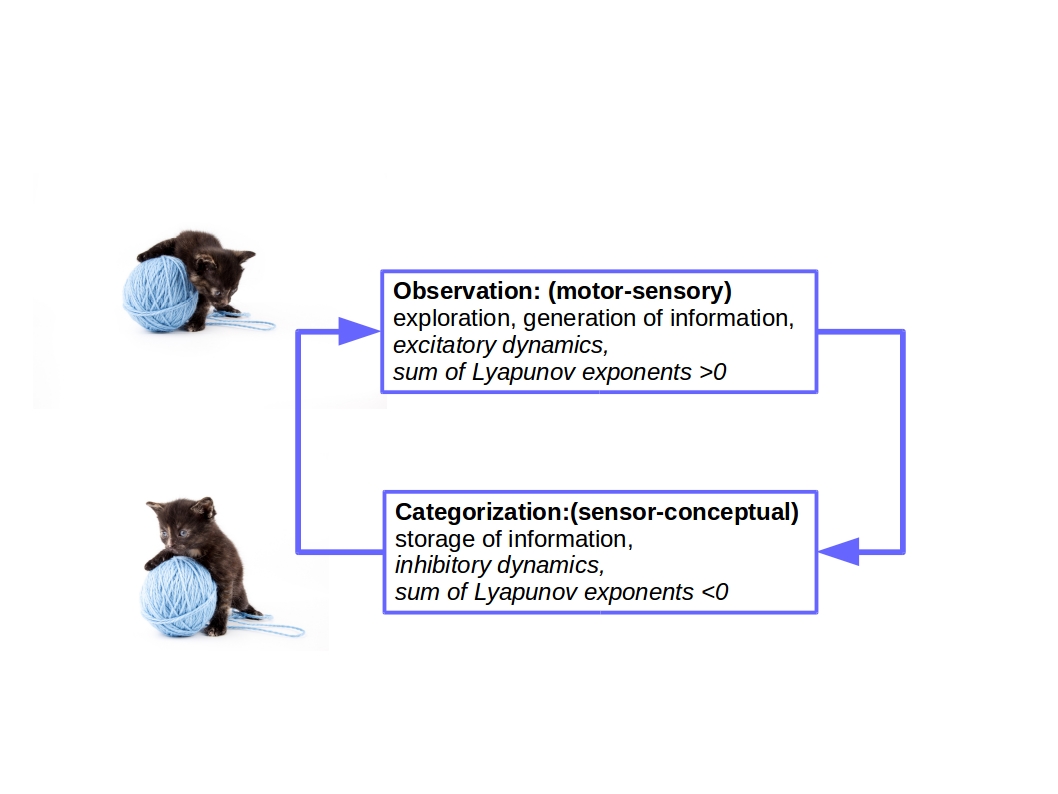
The whole process of creation and annihilation of attractors is best described as a “chaotic itinerancy” [Ikeda et al 1989, Kaneko & Tsuda, 2003; Tsuda, 2013, Grebogi et al 1987, Tsuda, 2001; Tsuda & Nicolis, 1999; Nicolis, J.S. & Tsuda, 1985]. Chaotic itinerancy describes dynamics where on the course of the evolution, due to parameter change and other fluctuations, attractors appear and disappear and while their basin boundaries follow the change. Most importantly, and for our focus too, is the inevitable existence of fractal-basin boundaries in such a itinerant process. It is exactly this coexistence of attractors with fractal basin boundaries that makes the act of partitioning of the impinging stimuli into various categories to potentially become ambiguous. A signal can be perceived in two very different ways, depending on history and context, and as to which attractor it will finally relax will be determined by the particular multistability conditions at the time, Fig. 2. A paradigmatic example of such ambiguity in perception is the famous “Necker cube”, where the “outside” figure can be apprehended “inside” in two ways, even oscillating between the two perceptions with no effort of deciding or judgement being performed aforehand.
Experimental Evidence
“Ambiguous figures can be found in any textbook about cognitive sciences and neuroscience.” This is how J. Kommeir and M. Bach put it in their review article, [Kornmeier & Bach, 2012] a very informative review about “what happens in the brain when perception changes but not the stimulus” which deals with the history and current affairs on this paradigmatic “gateway to perception”. Related to the bistabilty of the ambiguous perception and the resulting dual apprehensions of the Necker cube, oscillatory patterns were discovered and analysed by novel wavelet techniques on multi-channel data [Runnova et al. 2016]. In general, the investigations report that it takes a time interval of the order of 50ms (two loops of the feedback) in the recurrent neural activity present for the disambiguation of the image and a minimum of 350ms for the conscious perception and decision of the perceived reversal. Also, T. F. Arecchi and co-workers report on the characteristic time lapse between apprehension and judgement with experiments performed on Necker-cube figures as well as in literature and sound interpretation texts, eye-fixation and saccadic movement [Arecchi 2015; Arecchi, 2011; Arecchi, 2007].They report that short memory exhibits a characteristic time interval of 2-3s, justifying the discreteness of the process. In this 2-3sec interval the whole cycle of stimulus, response apprehension, judgement and awareness of the decision considered [Arecchi, 2016]. Their results of course vary depending on conditions, subjects and experimental settings. But what clearly emerges is that for each setting there is a specific, discrete and well defined time-interval governing the cognitive “decision making” processes during ambiguously perceived stimuli.
Figure 2. Chaos and Biological Information Processing. Adapted from [Nicolis J.S. & Tsuda, 1999]. “Outside” sends stimuli that can have more than one representations “Inside”. Categorization is possible due to coexisting attractors driven by a pacemaker in a “time-division-multiplexing-basis”. The whole process can be modelled as one of driven chaotic itinerancy. It can be implemented by very simple hardware giving rise to extremely complex software.
According to their findings, the process of apprehension has a duration around 1sec, at the maximum; it appears in EEG signals synchronized in the “gamma band” (frequencies between 40 and 60 Hz) coming from distant cortical areas. The process of judgement has a duration of about 2sec, as a comparison between two apprehensions and their judgement takes place. This is in the “alpha-band” and necessarily involves short memory to facilitate the comparison. Let us quote from [Arecchi, 2015] two examples that elucidate these two processes: “[apprehension:] a rabbit perceives a rustle behind a hedge and it runs away, without investigating whether it was a fox or just a blow of wind. … As Walter Freeman puts it the life of a brainy animal consists of the recursive use of this inferential procedure. …[judgement:] On the contrary, to catch the meaning of the 4-th verse of a poem, I must recover at least the 3-rd verse of that same poem, since I do not have a-priori algorithms to provide a satisfactory answer”. The process in the first example, with the rabbit, is automatic as it is based on existing available algorithms (a priori categories). For the process of the second example, with the poem, there can be no a-priori algorithms, as they have to be generated and performed “on the fly” depending on the challenge at hand (a posteriori attractor generation via a dynamic itinerancy).
Forward and Inverse Bayesian Inferences
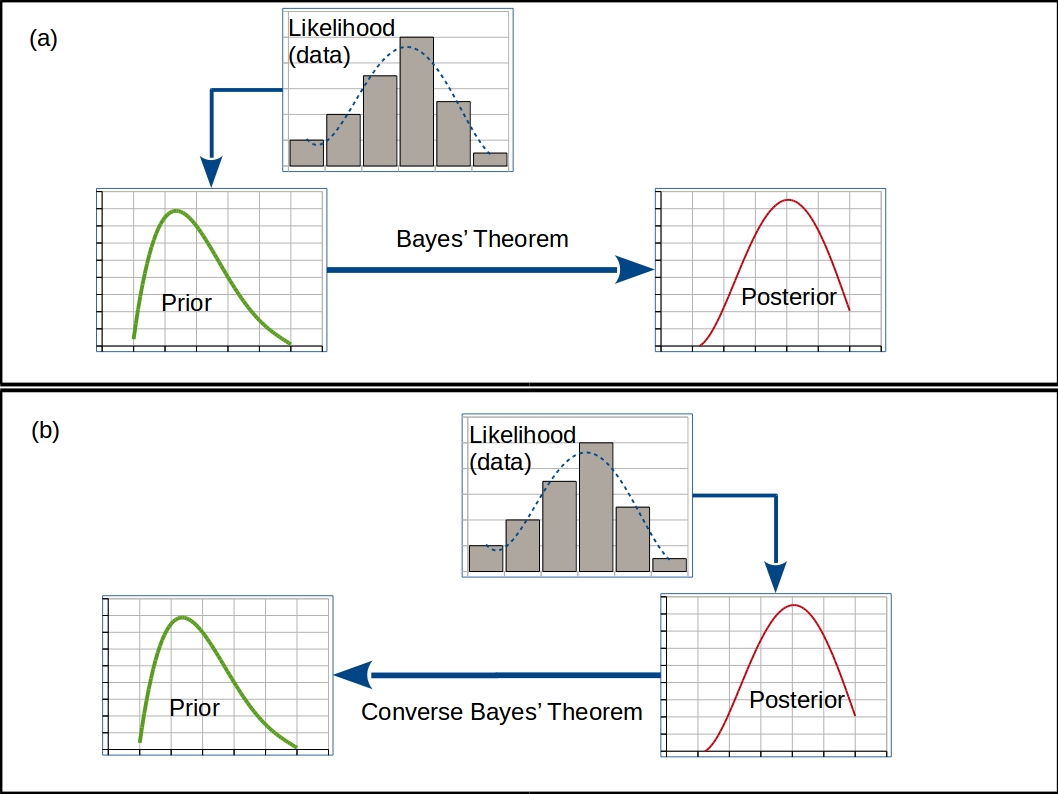
F. T. Arecchi further described the interpretation and apprehension of the sensory stimuli on the basis of available algorithms, through a (forward) Bayes inference and the comparison and judgement through an ‘Inverse Bayes inference’. For the (forward) Bayesian inference, (see Fig 3(a)), the standard setting involves the interpretative, competing, hypothesis, call it h, the sensory stimulus piece of data, d, the most plausible hypothesis, h*, which will eventually determine the reaction, and an a priori existing algorithm, P(d|h) which represents the conditional probability that a datum d is conforming with an hypothesis h. The conditional probabilities, P(d|h) are given e.g. have been learned during the past. They represent the equipment, or faculties, by which a cognitive agent faces and interprets its universe of discourse. So, this is a bottom up process, information flows from the input in neurons to the group(s) of neuronal correlates.
Therefore, following [Arecchi, 2015] apprehension can be implemented by a forward Bayes inference (Fig. 3a) given by Bayes formula:
P(h*) = P(h|d) = P(d|h) P(h) / P(d) (1)
Where P(h) is the prior probability of hypothesis h, d is the data, P(d|h) is the likelihood i.e. conditional probability that d results from h, P(d) is the evidence i.e. the probability that we observe the data d, and P(h*) = P(h|d) is the posterior conditional probability that Bayes theorem enables us to compute. The updating of P(h*) constitutes the basis of the Bayesian inference. The process is algorithmic, well posed and with a wide array of applications that become more and more numerous these days.
Figure 3. The Two Kinds of Inference due to Bayes. A schematic illustration of the two Bayesian inference processes: (a) the (Forward) Bayes’ Inference based on Bayes’ Theorem; a celebrated and standard hypothesis testing ‘toolbox’. (b) The Inverse Bayes Inference process based on the Converse Bayes’ Theorem; where, from a given posterior probability distribution and the likelihood, compatible prior probability distributions and their degree of plausibility can be ‘guessed’.
The inverse Bayesian inference, Fig. 3b, is based on the converse of Bayes Theorem or the so called “inverse Bayes’ formulae” [Arecchi, 2015; Ng, 2014, Ng & Tong, 2011; Tan et al, 2009]. We can state it, briefly, as determining the prior P(h) from which an observed posterior probability distribution P(h*) has resulted, given the likelihood P(d|h) of the data d. Of course, one can only start with a desired posterior as long as it’s logically compatible with the likelihood. So the converse Bayes’ Theorem is not automatically fulfilled by merely “solving for P(h)” Bayes’ formula above. Logical compatibility, consideration of convergence issues in a correctly chosen functional space and other subtleties are crucial. So the Inverse Bayesian inference is not guaranteed to mechanically converge or to have a unique solution. The Inverse Bayes Formulae do not yield automatically an algorithmic process for its solution. Based more on trial and error and ‘on the fly’ construction of step-by-step solutions the process can be characterized as non-computable, in the normal sense of the word. (See Fig. 3 for an illustration of the two Bayesian Inference processes).
Indeed is in accord with the nature of judgement as a “top-down” process since judgement involves comparison between (at least) two previous apprehensions, coded in a given language and recalled by memory. For example, as in [Arecchi, 2015; Arecchi, 2016], two successive pieces of the text can be compared and the conformity of the second one with respect to the first one can be determined. This is very different from apprehension, where there is no problem of conformity but of plausibility of h* in view of a motor reaction. As the non-mechanical and non-algorithmic nature of the construction of a judgement can be achieved by means of an inverse Bayes procedure [Arecchi, 2015; Gunji et al 2016, Gunji et al 2017], the observation that judgement entails “non-algorithmic jumps” is compatible as far as the inverse Bayesian inference process has to generate an ad hoc algorithm, build on the spot, data and context dependent, and by no means given beforehand.
Based on the above realization of the discreteness of the process Arrechi has conjectured for it a quantum-like character that yields a quantum-like constant. The “decoherence” or de-correlation time is compatible with the short term memory windows given by the experiments on linguistic understanding [Gabora & Aerts, 2002; Pothos & Busemeyer, 2009; Pothos & Busemeyer, 2013, Busemeyer & Bruza, 2012; Aerts & Aerts, 1995]. In He considered a “K-test” [Arecchi, 2015], as the time equivalent of Bell inequalities, and presented evidence as a case of pseudo-violation of the Leggett-Garg inequality [Arecchi et al, 2012]. Interestingly enough this is in accordance with the newest results from the field of “Quantum Cognition” where a quantum probability (following Von Neumann’s axioms) rather than the classic one (following Kolmogorov’s axioms) serve as the framework of understanding cognitive processes [Aerts & Sassoli de Biachi, 2015, Iⅈ Aerts, 2009; Aerts, et al, 2013; Aerts & Sozzo, 2011, Khrennikov, 2010; Khrennikov, 2007; Haven & Khrennikov, 2016; Gunji et al 2016; Gunji et al 2017].
A Minimal Model
Biological Information Dynamics in the face of ambiguities
As mentioned above the chaotic dynamics in biological processing consist of two phases: The phase (a) which is an exploration phase, characterized by expansion of the phase-space, with a positive sum of Lyapunov exponents, generating information and the phase (b) which is a categorization phase, characterized by contraction of the phase-space, with a negative sum of Lyapunov exponents, compressing and storing information. The whole process is that of a “chaotic itinerancy”, which means that attractors are created, modified and annihilated during both phases.
Therefore a minimal model for the biological information dynamics must incorporate a scheme for phases (a) and (b) that captures the essentials of both:
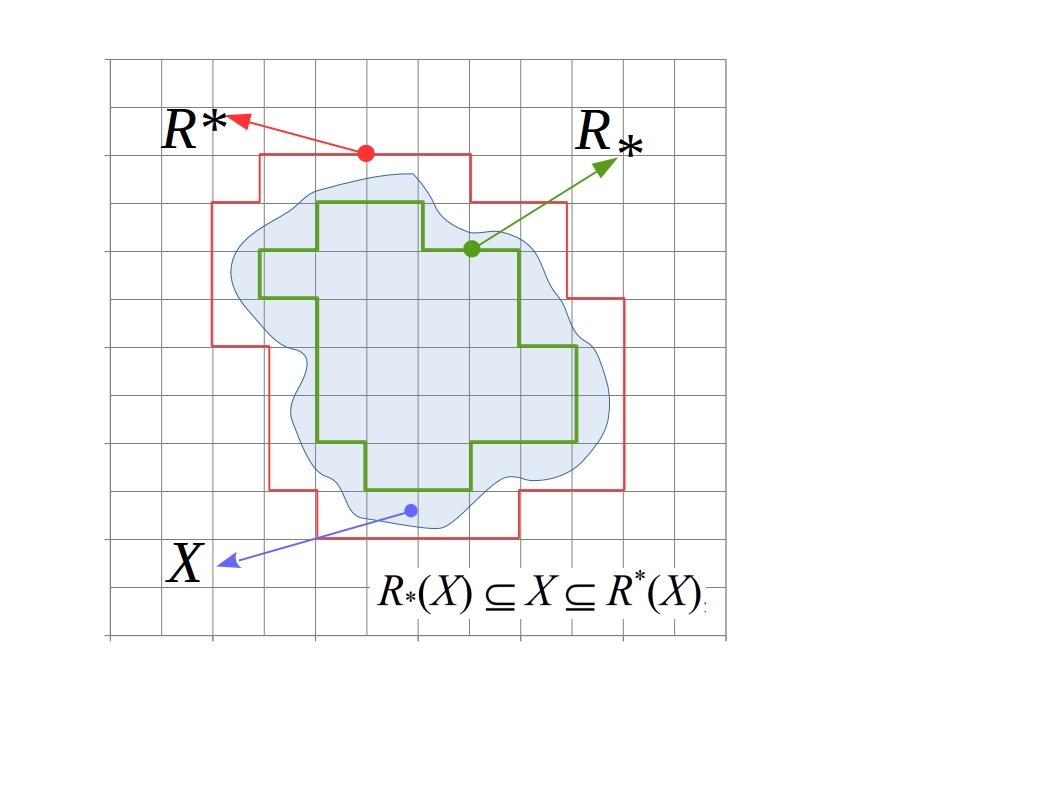
(a) For the expanding phase in order to describe the necessary coarse-graining of the sub-set of impinging stimuli that are captured by the organism’s sensors. We utilize a “Rough Set” approximation [Polkowski, 2002; Doherty et al, 2006] for the basin boundaries, Fig. 4. This way the volume of the phase space expands due to this coarsening and the plausible set of a priori probability distributions manifest augmented in number.
(b) For the contracting phase we employ an inhibitory network, modelling this way the compression of information required for categorization. The network can be a recursive network of the “restricted Botlzman machine” variety, famous for their dimensionality reduction capabilites and their utility in constructing “deep belief networks” [Hinton & Salakhutdinov, 2006; Hinton, 2009] based on the particulars of the rough set approximation. They are acting on the representations of the outside objects in the cognitive space ‘within’. The inhibitory network represents the coexisting cognitive attractors in their role as compressors of information [Gunji et al 2017].
The whole construction has been studied in detail, within its’ formal mathematical framework, in [Gunji et al, 2016; Gunji et al 2017]. Here we follow this work and review it in a comprehensive way. Therefore, as we will not go into the details of the mathematical concepts involved, we have to refer the interested reader to related citations.
Once a subset of stimuli has been captured we have a “universe of discourse” for the ‘outside’. Considering a set A to be the 'outside' consisting of objects, and let B be the 'inside' consisting of representations, and (minimally) two maps f,g :A→B to be a cognitive process relating outside objects to inside representations. We call x the object and we call f(x), g(x), its representations. An equivalence relation R on A is derived by a map, defined by xRy for x, yϵA such that f(x)=f(y) or g(x)=g(y) for that matter). It results in the 'outside' set of objects partitioned into a set of equivalence class such that
[x]R = {yϵA | xRy}. (2)
Three elements are essential elements for the construction of these maps: a way to choose a representative of a set of stimuli, a symmetry rule to deal with similarities and a locality principle for handing dissimilarities.
Figure 4. Rough Set Approximation. A rough set approximation, R, consists of its upper (R*) and lower (R*) parts. The inside of the red line defines an ‘Upper (R*) Rough Set Approximation’ of the set X, here shown with blue. The inside of the green line defines a ‘Lower (R*) Rough Set approximation’ of the same set X, hence the term ‘sandwiching’ i.e. R: R*⊂ X ⊂ R*
Let us give an example from [Gunji et al 2016]: Imagine that the 'outside' consists of a three cats one tabby, one white, and one black and two dogs, one white and the other black. The three cats as objects are mapped to their representative class CAT, (as a concept. The two dogs are mapped to their representative class DOG as a concept. This results in two equivalence classes, namely: {tabby cat, black cat, white cat} and {white dog, black dog}. Due to the axiom of choice [Lawvere & Rosebrugh, 2003; Lawvere, 1969] one can choose a tabby cat as a representative for the class CAT and a white dog as a representative for the class DOG. The symmetry law in the inhibitory network, for our example, implies that if an individual cat is not like a dog, an individual dog is not like a cat. Locality law implies that dissimilarity does not expand unnecessarily. So, if the case arises where a black cat is misclassified as a dog (due to poor vision, ambiguity, error, noise etc) it can only be taken to look like a black dog (evidently a very small black dog!).
More concretely: A sub-set of the outside world constitutes the “universe of discourse”. As the capture of the stimuli and their representations are subject to perturbations, noise, ambiguities and in general lack of complete knowledge for their characterization, we propose a “rough set” approximation [Pawlak, 1981; Pawlak, 1982] as the plausible minimal cognitive model, which will engulf these disturbances. Rough set theory and applications have been developed within soft-computing exactly with the aim to allow for ambiguous decisions along with other similar techniques such as “fuzzy set theory” [Zimmermann, 1992], from where it stemmed, which generalize the idea of set membership. This kind of ideas have been employed to the study of cognition with respect to discretized notions such as concepts, events and action selection. A rough set is an approximation of a normal (crisp) set and it can either contain or be contained by the original set. The intersection of an upper and a lower rough set approximation of a set, in a sense, sandwiches the original set and by blurring its boundaries allows ambiguity to be handled, see Fig 4.
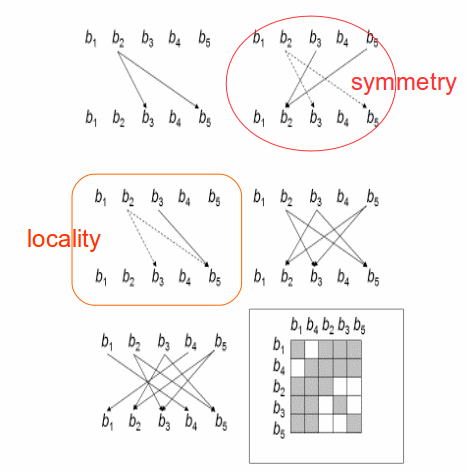
i) Firstly, they must establish a correspondence between the inside and outside a a representative concept. For this it is necessary we follow the “Axiom of Choice”, which states that for any set there exists a “choice function” allowing for a representative of the set to be chosen. Due to the axiom of choice one can choose one representative s for each equivalence class [x]R , i.e. [x]R = {yϵA | xRy} as in eq.(2).
ii) Secondly, they have to observe a “Symmetry Law”, Fig. 5. between themselves. Formally this is a property of the maps being equivalent classes. So, for their relations holds that: if elements ”a” and “b” are in a relation “~”, then b is in a relation “~” with “a” too. Formally: (a~b) iff (b ~ a).
iii) Thirdly, the maps must obey a “Locality Rule”, Fig. 5, that is if two elements (a,b) are mapped coming from an element c and one of them, say b, is also mapped from an element d which happens to be a ‘neighbour of c’, then d must be mapped to a too. Formally: If (c→ a and c→b and d→b) and (d neighbour of c), then d→ a.
Choosing the maps in this way we obviously establish a one-to-one correspondence between the 'inside' and 'outside' if one neglects objects but not their representatives, Fig. 6. The outside is, however, not trivial a priori. Objects are gradually and empirically identified as such a posteriori, this suggests that is difficult for us to map objects to representations easily. We have explored the formal framework of such considerations in [Gunji et al 2016, Gunji et al 2017]. In last analysis an a priori probability is itself an attractor as in determining an a priori probability much action, trial and error and a converging process is necessary [Nicolis & Tsuda, 1999; Gunji, 1997]. We will return on this issue latter, in Sec. 5, as we examine the, so called, "inverse Bayesian inference".
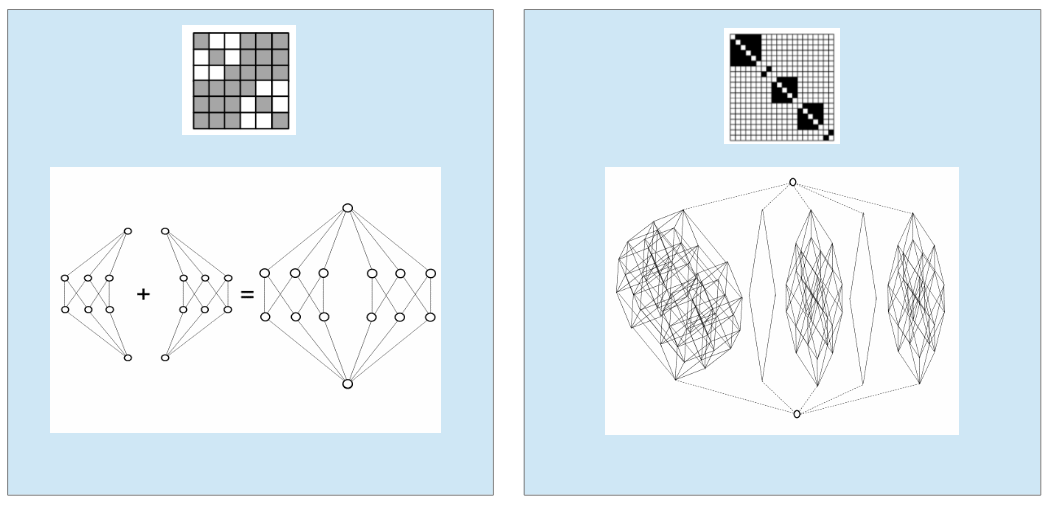
Figure 5. Network Rules. An illustrative example of the construction of a directed inhibitory network. Two partitions of a set of the representatives, here {bi}(i=1…5) assumed that are coming from the same stimulus, form a binary relation. Initially one vertex is chosen randomly and edges whose source is a chosen vertex are also randomly chosen (top left). By using the symmetry (top right) and locality rules (middle left) a local network is obtained (middle right). Successively applying the procedure for all elements leads to a directed inhibitory network (left bottom) which then can be expressed in a block-diagonal matrix form (right bottom).
Closing the loop: ambiguous representation implemented by two maps
In the simplest case of a bistable ambiguity in representation, recall the Necker cube, see also Fig. 2, we have weakening of the axiom of choice of a representative as it cannot be chosen in a unique way. This ambiguous choice can be defined by the action of two maps, which correspond to the basic, minimal, set of two coexisting attractors. Let the maps be f and g and the equivalence relations derived from f and g be R and K, respectively. Since a cognitive process g conflicts f for some (not all) xϵA (i.e. f(x)≠g(x)), the definition of g has to be considered under a particular condition of an inhibition equipped with a symmetry and a locality law in order to allow for similarities and contain dissimilarities, as mentioned above. These laws are outlined in detail in Sec. 3.2 of [Gunji et al, 2016].
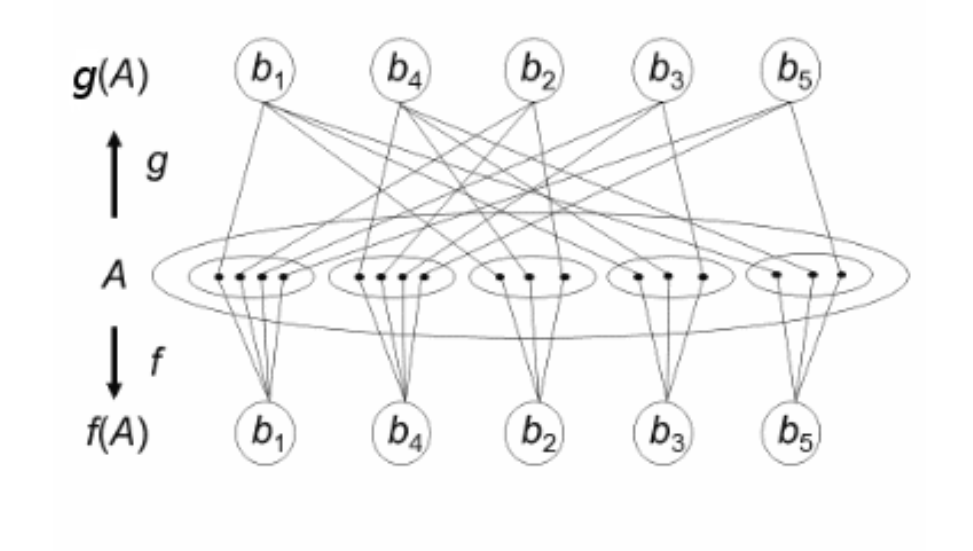
Let the elements of f(A) to be b1, b2, …, bn (representation with respect tof). A representation (an element of f(A)) derives an equivalence class (a subset of A) which has no intersection with each other, therefore it is a partition. We here denote a partition derived by bkwith respect to f as bkf = {x ⊆ A | f(x)=bk}. Similarly an equivalence class with respect to g:A→ f(A) is denoted by bkg. Example of such partitioning and the action of symmetry and locality rules in the construction of the inhibitory network’s nodes and edges are illustrated in Fig. 5 and detailed in [Gunji et al, 2016, Gunji et al, 2017].
The secondary map g, which is defined in accordance to the directed inhibitory network, allows the relation between equivalence classes (i.e. partitions with respect to f and g respectively) to be rearranged in a particular matrix which consists of various diagonal matrices, Fig. 5 and Fig. 6. The algorithm is a straight forward row-column rearrangement and this way the construction is completed by the representation of the partitions of the inhibitory network as a adjacency-type of matrix as shown in Fig. 5 bottom right. The matrix is simply constructed as follows: Take an element of a matrix at a column bj and a row bi. If there is a link between biand bj, in the inhibitory network, then a component at (bi, bj) is zero (0, white box in the figure), and otherwise it is one (1, black box in the picture). This matrix is symmetric matrix with diagonal elements equal to 1 and the off-diagonal entries are either 0’s or 1’s depending on the network.
Phases (a) and (b) constitute a closed loop of repeated operations in a nonlinearly recursive fashion [Nicolis & Tsuda, 1999]. So for completing the process we need to collect the fixed points of the matrix, closing the loop, by repeated applications of a nonlinear recurrence which will lead to a temporary but stable perception of the outside.
Rough set approximation is crucial in achieving this task. The main idea can be summarized as follows: the two partitions of the set {b} of representatives, {bf}, {bg} (dropping the subscript indexes for shorthand) are induced by an equivalence (class) relation each, say R for f: {bf} and K for g: {bg}; both derived, of course, by the inhibitory network. Both R and K can be approximated by their upper (denoted as R* and K*, respectively) and lower (R* and K*) rough sets. It is instrumental to keep in mind that if an equivalence class is compared to a neighbourhood in topology, upper approximation is analogous to closure where the lower approximation is analogous to the set of the interior points in topology. So, a set is effectively sandwiched in-between its’ lower and upper approximation, Fig. 4, analogous to the ‘coarse graining’ techniques familiar from nonlinear dynamics [Basios & MacKernann, 2011].
Now we can investigate the fixed points of all possible compositions related to the closed-loop recurrence. To start, we consider the four kinds of elementary compositions, R*K*, R*K*, R*K* and R*K*. Now we can ask whether a partition is allowed as a fixed point. For the case of R*K* it turns out that R*K*(b1f ) = A. The whole set! This implies that a partition b1f is not a fixed point with respect to R*K*. Next we consider the case, R*K*. As it turns out, R*K*(b1f ) = ø. The empty set! Therefore it follows that b1f is not a fixed point with respect to R*K*. But for the cases of R*K* and R*K* composition, it turns out that R*K*(b1) =b1f . As this verification can be generalized to any number of partitions we can say that any partition with respect to f can be a fixed point X for the equation, and similarly for R*K*
R*K*(X) =X and R*K*(X) = X
The same holds for all four basic combinations of compositions:
R*K*(X) =X, R*K*(X) =X, K*R*(X) =X and K*R*(X) =X (3)
Moreover, we observed that since the collection of fixed points {X}, with X being a subset of A, are ordered by inclusion each defines a lattice [Davey, & Priestley, 2002; Birkhoff, 1967; Svozil, 1993; Svozil, 1998] whose partial order is defined by inclusion, formally written as (<L, Í >) and that all lattices defined by any collection of fixed points for the elementary compositions are isomorphic to one another. Lattices are mathematical structures, partially ordered sets, that serve as the basis for logic [Birkhoff, 1967; Davey & Priestley, 2002, Kalbach; 1983, Gunji et al 2009; Gunji & Haruna, 2010; Svozil, 1998]. We shall return to this remark in Sec. 6 where we estimate the logic of a universe of discourse that includes ambiguous representations.
Nonlinear Biological Information processing as Bayesian Inferences
Now we are able to show that our work is consistent with a quantum-like theoretical conjecture proposed by Arecchi and discussed in Section 2. As mentioned before, decision to an external stimulus could result from a choice of a neural group which can give rise to largest synchronized and distributed domains of correlates. Such a process of apprehension can be implemented by (forward) Bayes inference as proposed by Arecchi, eq. (1). Bayesian inference is often compared to a process of climbing a mountain within a landscape of coded data searching by using only local information, P(h*) provides the next plausible climbing step obtained from the previous step, P(h), provided by the data from an external stimulus, P(d), and especially of the external stimulus received at the position of the previous step, P(d|h). If an isolated unique stimulus is given, the process of data apprehension occurs.
When two successive stimuli are given within a specified short term, the first apprehension stored is retrieved and is compared to the second one. Thus it can give rise to the process of judgement. If this process is also to be compared to the climbing of a mountain within a landscape of coded data, the mountain would contain multiple peaks which prohibits a climber only with local view to climb to the globally highest peak. Globally optimum solution cannot be obtained only via a logical computation based on Boolean logic but by a ‘non-logical’ jump. According to [Arecchi, 2015], the non-logical jumps appearing in cognition provide evidence for quantum-like effects, and this is implemented by an inverse Bayes inference. From equation (1), the inverse Bayes inference is expressed, formally, as
P(d|h) = P(d) P(h*) /P(h). (4)
Where now the data (d) and a posteriori hypothesis (h*) represent the current stimulus and the previous one, respectively. The most suitable algorithm, P(d|h) that best matches d and h* is obtained by an inverse Bayes inference. Observing the restrictions of convergence issues, compatibility with the likelihood etc as required by the converse Bayes’ Theorem and since the inverse Bayes inference contains non-algorithmic jump, P(d|h) is not a simple modification of the formula from eq.(4) but an equation obtained from a modification of the hypothesis, P(h). Therefore, P(d|h) cannot be obtained by simple iterations of recursive process, hence its non-algorithmic nature.
Inverse Bayes inference proposed by [Arecchi, 2015] can be compared to our cognitive model based on ambiguous representation. First we replace terms in Bayes inference by our data and approximations. Because a given set of data d in Bayes inference can be replaced with a given subset X in a universal set A, and because its lower and upper approximations for X have the following order, i.e. they are sandwiching the subset X: R*(X) ⊆ X ⊆ R*(X), data coupled with a priori hypothesis such as P(d|h) can be replaced by the upper approximation, R*(X), and data coupled with a posteriori hypothesis such as P(h|d) = P(h*) can be replaced by the lower approximation, R*(X). Since any element in the lower approximation is in X, and only some elements in the upper approximation are elements of X, the lower and upper approximation correspond to the sufficient and necessary conditions, respectively. That is why the upper and lower approximation could be considered to correspond to the a priori and a posteriori hypotheses, respectively.
How is the (forward) Bayesian inference implemented in our ambiguous representation? In eq. (4), h is replaced by equivalence relation, R derived by a particular representation (map), P(d|h) is replaced by R*(X), and P(h|d) = P(h*) is replaced by R*(X). Therefore, Bayesian inference is the process of computing R*(X) from R*(X) (i.e. from a priori to a posteriori). So as to achieve this computation data, X, is implemented by a particular form because R* is used instead of an equivalence class, [x]R.
Similarly, the inverse Bayes inference is the process of computing R*(X) from R*(X) i.e. from a posteriori to a priori [Ng, 2014]. However, in order to do that we need an extra equivalence relation, K, with a particular relation between equivalence classes with respect to K and R, including a condition for its lower rough set approximation, such that K*(Y) = [x]K where R*([x]K) = Y, making possible that we get a fixed point, Y, under R* and K* , formally expressed as R*(Y) =R*(K*(Y))=Y which would have not exist for the action of R* alone.
This is exactly the condition which is satisfied by our pair of equivalence relations derived by the pair of maps, f and g under a constraint of an inhibitory network equipped with symmetry and locality. It is crucial in comparing our model to that of Arecchi’s that a collection of fixed points is naturally introduced for both R and K in order that the combined action of their upper and lower rough set approximations will take care of convergence issues [Gunji et al, 2017]. This way one can have well defined prior and posterior probability distributions participating in the Bayesian Inference either forward or inverse.
Compared to the inverse Bayesian inference, to compute an a priori hypothesis R*(Y), a non-algorithmic jump related to quantum-like effects corresponds to replacing a relation R by another relation K. This amounts to the modification of the original hypothesis. Which is a jump clearly “non-algorithmic” (or better, non-mechanical) and non-boolean in terms of logic, reminiscent of the quantum-like postulate of Arecchi and the (non-Boolean) quantum logic implemented in the area of “Quantum Cognition” [Aerts et al, 2013; Aerts & Sassoli de Biachi, 2015; Pothos & Busemeyer, 2009, Busemeyer, & Bruza, 2012; ].
The Logic of Ambiguous Representations
The inverse Bayesian inference can be implemented by equation which contains a non-Boolean logical jump such as the modification of the original hypothesis (i.e. a novel equivalence relation) from R to K. The matrix representation of the inhibitory network (Fig. 5, Fig. 6) allows for the classification of the lattice where the logic of the whole process is based, Fig. 7. As we have proved in [Gunji et al 2016, Gunji et al 2017] a lattice resulting from a collection of fixed points satisfying R*(K*(Y))=Y is an “orthomodular” lattice [Davey & Priestley, 2002]. Orthomodular lattices are the ones underlying quantum logic [Birkhoff & Von Neumann, 1975; Piron, 1976; Svozil, 1998; Engesser et al, 2009] and constitute a generalization of the Boolean lattice where Boolean (classical) algebras are based. As a representation follows rules of composition and other operations. The logic of a representation captures essential properties of both set operations and logic operations. The most familiar of all logical structures is the Boolean logic, a mathematical structure widely known from computer operations. The idea that the propositions of a logic are based on a “lattice structure”, signifying a partial order of their sets, was first introduced with the works of Boole and Pierce, “seeking an algebraic formalization of logical thought processes”, already in the mid 19th century. A lattice is a partially ordered set closed with respect to meet and join operations of two elements, where the join of two elements is the least element which is larger than both of two elements and the meet of two elements is the greatest element which is smaller than both of two elements [Birkhoff, 1967; Davey & Priestley, 2002; Kalbach, G. (1983)].
Figure 6. Network Construction From the Two Partitions of the Set of Representatives. Inhibitory network constructed from a set of objects, A (stimuli). A pair of maps, f and g, induce the two partitions, f(A) and g(A) respectively, for the set of representations {bi}(i=1…5) of A. Each is on its own rough set approximations, R = (R*, R*) for f and K = (K*, K*) for g. Given the initial map f:A→B, the other map g is accordingly determined so as to satisfy the same rules of the directed inhibitory network.
The lattices of the a collection of the fixed points of the representation discussed above are ordered by inclusion. The meet here is defined by intersection, and the join is defined by union. In other words, any of the concepts in a set lattice can be constructed for all possible combinations of atom-concepts which are partitions of the representations. We note that the set lattice or a Boolean algebra is represented simply by a diagonal matrix between partitions.
Orthomodular Lattices & Quantum-Cognition
Hasse diagrams help us visualize partially ordered sets, such as lattices, and easily identify the kind of logic that are based on [Davey & Priestley, 2002; Engesser et al., (2009)]. A Boolean lattice coming from the diagonal matrix between is symmetric without loops. An orthomodular lattice, like the ones in quantum logic, is defined by an almost disjoint union of Boolean algebras. Especially if it contains no loop, it is an orthocomplemented lattice (Boolean algebras being a special case of orthocomplemented lattices). It shows that LD is an orthomodular lattice, and it is also an orthocomplemented lattice. The matrices that come from the partitions of the sets of the representatives, {bf} and {bg} above, are symmetric with all their diagonal elements equal to 1 and off-diagonal elements arranged in symmetric sub-matrices (see Fig. 7).
This implies that they have resulted based on an (orthocomplemented) but most importantly an orthomodular lattices and therefore have non-Boolean (quantum) logics as their bases. Example of Hasse diagrams coming from our scheme outlined above and detailed in [Gunji et al 2016; Gunji et al 2017] are shown in Fig. 7.
The left panel of Fig. 7 shows a lattice derived from a 6-by-6matrix. Since a matrix consists of two diagonal blocks, a lattice is a quasi-disjoint union of two Boolean algebras. Each diagonal matrix contains three diagonal elements, and that shows a 23-Boolean algebra. Each element of a lattice is represented by a circle in Hasse diagram as shown. If X⊆Y, an element X is located below an element Y, and if there is no element between X and Y, two elements are linked by a line. Each lattice consisting of eight elements represents 23-Boolean algebra. The greatest, (X=A) in the top, and the least element (X=ø) in the bottom of the diagram are common to both of the two 23-Boolean algebras. The lattices corresponding to the matrix in the insets above the panels of Fig. 7 are represented by their Hasse diagrams found bellow. This kind of Hasse diagram implies that the lattice is orthocomplemented and orthomodular.
Similarly, the right panel of Fig. 7 shows a Hasse diagram of a lattice corresponding to a larger matrix, which means a construction with a bigger population of representatives in the partitions. Since a matrix consists of a diagonal matrix containing six elements, two diagonal matrices with five elements or two elements, a lattice consists of one 26-Boolean algebras, two 25-Boolean algebras and two 22-Boolean algebras. Broken lines are used to indicate that the greatest (A) and least elements (ø) represented by circles are common to all block lattices, yet they are not used to indicate inclusion relation or order. Once again, the above testifies that the lattice at hand is an orthomodular (and orthocomplemented) lattice.
Figure 7. The logical structure for the sets of fixed points demonstrated by Hasse Diagrams. Left panel: two diagrams connected by the symbol “+” show two Boolean algebras obtained from two blocks from the matrix (shown in the inlet above it). The whole matrix is an ‘almost disjoint union’ of the two Boolean algebras, where the least (the empty set) and the greatest (the whole set X) elements are common to both Boolean algebras. Right panel: Hasse diagram of a lattice obtained from a matrix shown in Figure 6 above. A matrix consists of five off-diagonal blocks. The whole diagram corresponding to this matrix (shown in the inlet above it) is an almost disjoint union of five Boolean algebras. The Hasse sub-diagrams of each Boolean algebra correspond to each block in the given matrix. Here only the least (the empty set) and the greatest (the whole set X) elements common to both Boolean algebras are represented by circles.
According to the theory of quantum logic [Birkhoff & Von Neumann 1969], the closed subspace of a Hilbert space formulation of quantum mechanics forms an orthomodular lattice. As they put it, they are "formally indistinguishable from the calculus of linear subspaces (of a Hilbert space) with respect to set products, linear sums and orthogonal complements" corresponding to the operations “and”, “or” and “not” in Boolean lattices. An orthomodular lattice is of crucial importance to quantum logic [Kalbach, 1983; Svozil, 1993; Svozil, 1998]. After this realization quantum logic became a core issue in physics and mathematics but after the seminal work of Aerts and co-workers, since the early `90s, it became an very important and widely discussed theme of investigation in the realm of human cognition. Recently theoretical and experimental advances in the area of quantum cognition and decision making highlight more and more the quantum-like nature of conceptualization. Amassing results from a wide array of disciplines, as from cognitive mathematical psychology [Pothos & Busemeyer, 2013], operational research and 'rational decision theory' [Pothos & Busemeyer, 2013], finance [Segal & Segal, 1998; Baaquie, 2004], experimental and theoretical artificial intelligence [Aerts &Czachor, 2004; Gabora & Aerts, 2002] and many other fields [Khrennikov, 2010], quantum probability's logical structure and quantum-like behaviour in cognition and/or concept correspondence have been developed in several publications by a considerable community of authors [Busemeyer & Bruza, 2012]. We would like to just briefly mention that it came as a pleasant surprise to us that the key ideas on the role of chaos in biological information processing and especially of “chaotic itinerancy” discussed above, the “non-algorithmic” jumps in inverse Bayesian inference and quantum logic share a common denominator when ambiguous representations are seen in a detailed and formal manner.
Conclusions
In this work we revisited the role of chaos in biological information processing and we focused on the presence of ambiguous stimuli and what their perception entails. Recent results and experimental evidence in favour of the importance of the phenomenon were also briefly reviewed. We reformulated the (forward and inverse) Bayesian inference argument about apprehension and judgement in terms of a rough set approximation. We did this by utilizing an inhibitory network, mimicking the expanding and contracting dynamics which is a central premise for chaotic dynamics as applied in biological information processing. In the course of our investigation we found that the underlying logic is a non-Boolean, essentially quantum, logic. Our exposition summarizes these results based on our previous detailed formal exposition where all the mathematical details are available.
The main conclusion is that by bringing together these three seemingly independent ways of thinking (dynamical, Bayesian and set-theoretic) about the ubiquitously present perception of ambiguous concepts, images or stimuli in general, reveals that biological information processing and its dynamics is still a promising and a highly non-trivial affair. We believe that a very fertile ground still lies in front of such investigations, rich in important realizations about the nature of perception and open to many possible applications.
| Attachment | Size |
|---|---|
| 1.37 MB |
Special thanks to Professors Andrey Shilnikov (Georgia State), Dmitri Turaev (Imperial College), Jean-Louis Deneubourg (ULB), D. Aerts (VUB) and Maximiliano Sassoli de Biachi (VUB) for fascinating & inspiring discussions. We dedicate this review to the late teacher of us J. S. Nicolis with the fondest memories.
Aerts, D. and Aerts, S., (1995): “Applications of quantum statistics in psychological studies of decision processes”, Foundations of Science, 1, pp. 85-97
Aerts, D. and Sassoli de Bianchi, M., (2015): “The unreasonable success of quantum probability: Part I & II” J. Math. Psychology, Vol. 67, August 2015, pp. 51-75 & pp. 76-90
Aerts, D. and Sozzo, S., (2011): “Quantum structures in cognition: Why and how concepts are entangled”. Lecture Notes in Computer Science, 7052, pp. 118-129, Springer.
Aerts, D., (2009): “Quantum structure in cognition”. J. Math. Psychology, Vol. 53, pp. 314-348.
Aerts, D., Broekaert, J., Gabora, L. and Sozzo, S., (2013): “Quantum structure and human thought”. Behavioral and Brain Sciences, 36, pp. 274-276.
Aerts, D., Gabora, L. and Sozzo, S., (2013): “Concepts and their dynamics: A quantum-theoretic modeling of human thought”. Topics in Cognitive Science, Vol 5, pp. 737-772.
Arecchi F. T., (2007): “Physics of cognition: complexity and creativity”, Eur. Phys. J. Special Topics vol. 146, 205.
Arecchi F. T., (2011): “Phenomenology of Consciousness: from Apprehension to Judgment”, Nonlinear Dynamics, Psychology and Life Sciences, vol. 15, pg. 359-375.
Arecchi T. F., Farini A., and Megna, N., (2016): “A test of multiple correlation temporal window characteristic of non-Markov processes” , European Phys. J. Plus 131:50.
Arecchi T. F., (2015): “Cognition and language: from apprehension to judgment-Quantum conjectures”, Chap. 15, (pp. 319-344), in "Chaos,Information Processing and Paradoxical Games" (Nicolis G. and Basios V., eds), World Scientific.
Arecchi, F. T., Farini, A., Megna,N., Baldanzi, E,., (2012): "Violation of the Leggett-Garg inequality in visual process" Perception 41 ECVP Abstract Supplement, p. 238.
Babloyantz A. and Destexhe A., (1986): Low-dimensional chaos in an instance of epilepsy. Proceedings, National Academy of Sciences USA, vol. 83, pp-3513-3517.
Basios, V. and Mac Kernan, D., (2011): “Symbolic dynamics, coarse graining and the monitoring of complex systems”. Int. J. of Bifurcation and Chaos, vol. 21 (12), pp.3465-3475.
Birkhoff, G and Neumann, J.V., (1975): The logic of Quantum Mechanics. In The Logico-Algebraic Approach to Quantum Mechanics (Hooker , C.A. (ed.)), Springer. pp.1-26.
Birkhoff, G. (1967): “Lattice theory”, Vol. 25, American Mathematical Soc.
Busemeyer, J.R. and Bruza, P.D., (2012): “Quantum models of cognition and decision”, Cambridge University press.
Davey, B. A., and Priestley, H. A. (2002): “Introduction to lattices and order”: Cambridge University press.
Doherty, P., Lyukaszewicz, W., Skowron, A., and Szalas, A., (2006): “Knowledge Representation Techniques, A rough Set Approach”. Springer-Verlag, Berlin.
Engesser, K., Gabbaym D.M. and Lehmann, D., (2009): “Handbook of Quantum Logic and Quantum Structures: Quantum Logic”, Elsevier.
Freeman W.J., (2015): “Thermodynamics of Cerebral Cortex Assayed by Measures of Mass Action”, Chap. 13, (pp. 277-300), in "Chaos,Information Processing and Paradoxical Games" (Nicolis G. and Basios V., eds), World Scientific.
Freeman W.J., (2013): “How brains make up their minds”, Columbia University press.
Freeman W.J., Livi R, Obinata M, Vitiello G. (2012): Cortical phase transitions,non-equilibrium thermodynamics and the time-dependent Ginzburg-Landau equation. Int. J. Mod. Phys. B 26, 1250035.
Freeman, W. J., (2000) “Neurodynamics : an exploration in mesoscopic brain dynamics”, (Perspectives in neural computing), Springer Verlag.
Gabora, L. and Aerts, D. (2002): “Contextualizing concepts using a mathematical generalization of the quantum formalism”. Journal of Experimental and Theoretical Artificial Intelligence, 14, pp. 327-358
Grebogi, C., Ott, E. and Yorke, J.A. (1987): “Basin Boundary Metamorphoses: Changes in Accessible Boundary Orbits”, Physica D, 24:243.
Gunji, Y-P., Sonoda, K. and Basios, V., (2016): “Quantum cognition based on an ambiguous representation derived from a rough set approximation”, BioSystems Vol. 141, pp.55–66.
Gunji, Y-P., Shinohara, S. and Basios, V., (2017): “Inverse Bayes inference is a Key of Consciousness featuring Macroscopic Quantum Logical Structure”, Biosystems Vol. 152, pp. 44-55.
Gunji, Y-P., Ito, K. and Kusunoki, Y. (1997): “Formal model of internal measurement: alternate changing between recursive definition and domain equation”. Physica D 110:289-312.
Gunji, Y.-P. and Haruna, T. (2010): “A Non-Boolean Lattice Derived by Double Indiscernibility”. Transactions on Rough Sets, vol. XII, pp211-225.
Gunji, Y.-P., Haruna, T. and Kitamura, E.S. (2009): “Lattice derived by double indiscernibility and computational complementarity”. Lecture Notes in Artificial Intelligence, vol. 5589, pp.46-51.
Haken, H. (1996): “Principles of Brain Functioning”, Springer, Berlin.
Haken, H. (2008), “Self-organization of Brain Function”, Scholarpedia, 3(4):2555.
Haven, E. and Khrennikov, A., eds., (2016): “Quantum probability and the mathematical modelling of decision making”, Phil. Trans. R. Soc. A (Theme issue), vol. 374, pp.2058.
Hinton, G. E.; Salakhutdinov, R. R., (2006): "Reducing the Dimensionality of Data with Neural Networks". Science. Vol. 313 (5786), pp504–507.
Hinton, G.E., (2009): “Deep belief networks”, Scholarpedia, 4(5):5947.
Hizanidis J., Kouvaris N.E, Zamora-Lopez G., D'iaz-Guilera A. and Antonopoulos C.G., (2016): “Chimera-like States in Modular Neural Networks”, Scientific Reports, v6, p.19845. DOI:http://dx.doi.org/10.1038/srep19845.
Ikeda K, Otsuka K, Matsumoto K, (1989): “Maxwell-Bloch turbulence”, Prog Theor Phys Suppl 99: 295-324.
Izhikevich, E.M., (2004): “Which Model to Use for Cortical Spiking Neurons?”. IEEE Transactions On Neural Networks, Vol. 15, No. 5, pp.1063.
Kalbach, G. (1983): “Orthomodular Lattices”. Academic Press, London, New York.
Kaneko K, Tsuda I., eds, (2003): “Focus issue on chaotic itinerancy”, Chaos 13: 926-1164.
Katz B. (1971) : Quantal Mechanism of Neural Transmitter Release", Science 173, 123-126
Khrennikov A.Y. (2007): “Can quantum information be processed by macroscopic systems?” Quantum Information Processing, Vol. 6, pp.401-429.
Khrennikov, A.Y., (2010): “Ubiquitous Quantum Structure: From Psychology to Finance”, Springer
Kornmeier J., Bach, M., (2012): “Ambiguous Figures – What Happens in the Brain When Perception Changes But Not the Stimulus”, Frontiers in Human Neuroscience, Vol. 6, Article 51. DOI:10.3389/fnhum.2012.00051
Lawvere, F.W, and Rosebrugh, R., (2003): Sets for mathematics. Cambridge University press.
Lawvere, F.W., (1969): Diagonal arguments and Cartesian closed categories. Category theory, homology theory and their applications II. Springer Berlin Heidelberg, 134-145.
Meunier, D., Lambiotte, R. and Bullmore, E. T., (2010): “Modular and hierarchically modular organization of brain networks”. Front. Neurosci. 4, 200 (2010).
McDonnell, M. and Stocks, N., (2009), “Suprathreshold stochastic resonance”, Scholarpedia, 4(6):6508.
Mori T and Kai, S., (2002): Noise-Induced Entrainment and Stochastic Resonance in Human Brain Waves Phys. Rev.Let. 88(21):218101; DOI: 10.1103/PhysRevLett.88.218101
Ng, K. W. and Tong, H., (2011): “Inversion of Bayes formula and measures of Bayesian information gain and pairwise dependence”, Statistics and Its Interface, Vol. 4, pp.95–103.
Ng, K. W.,(2014): “The Converse of Bayes Theorem with Applications”, Wiley.
Nicolis J.S., (1986): “Dynamics of Hierarchical Systems: An Evolutionary Approach”, Springer Series in Synergetics.
Nicolis J.S., (1991): “Chaos and Information Processing: A Heuristic Outline”, World Scientific.
Nicolis, G. and Basios, V., (2015): “Chaos Information Processing and Paradoxical Games: The legacy of J. S. Nicolis”, World Scientific.
Nicolis, G. and Nicolis, C., (2012): “Foundations of Complex Systems: Emergence, Information and Prediction”, Word Scientific.
Nicolis, J.S. and Tsuda, I., (1985): “Chaotic dynamics of information processing: The 'magic number seven plus-minus two' revisited”, Bulletin of Mathematical Biology, vol. 47, no. 3, pp. 343-365.
Nicolis, J.S., Mayer-Kress, G. and Haubs, G. (1983): “Non-Uniform Chaotic Dynamics with Implications to Information Processing”, Z. Naturforsch 38A, 1157-1169.
Pawlak, Z., (1981): “Information systems-theoretical foundations”. Information Systems, Vol. 6, pp. 205-218.
Pawlak, Z., (1982): “Rough Sets”. Intern. J. Comp. Inform. Sci., Vol. 11, pp. 341-356.
Peres, A., (1999): “Bayesian Analysis of Bell Inequalities”, Fortschritte der Physik , Vol. 48, pp.5-7.
Piron, C., (1976). “Foundations of Quantum Physics”. Massachusetts: W.A. Benjamin Inc.
Polkowski, L., (2002): “Rough Sets: Mathematical Foundations”. Physica-Verlag, Springer, Heidelberg. DOI: http://dx.doi.org/10.1007/978-3-7908-1776-8
Pothos, E.M. and Busemeyer, J.R., (2013): “Can quantum probability provide a new direction for cognitive modeling?”. Behavioral and Brain Sciences, 36, pp. 255-274.
Pothos, E.M., Busemeyer, J.R., (2009): “A quantum probability model explanation for violations of ‘rational’ decision theory”. Proceedings of the Royal Society B, 276, pp. 2171-2178.
Runnova, A. E., Pisarchik, N., Zhuravlev M.O., Koronovskiy, A. A., Grubov, V. V., Maksimenko V. A. and Hramov, A. E. (2016): “Experimental Study of Oscillatory Patterns in the Human Eeg During the Perception of Bistable Images”, Opera Medica & Physiologica, Issue 2, pages 112-116. DOI:10.20388/OMP2016.002.0033
Shaw, R., (1981): “Strange attractors, chaotic behavior, and information flow,” Z. Naturforsch 36A, 80-112.
Shilnikov, A. and Turaev, D., (2007): “Blue Sky Catastrophe”, Scholarpedia, 2(8):1889.
Shilnikov, A., Cymbalyuk, G., (2005): “Transition between tonic-spiking and bursting in a neuron model via the blue-sky catastrophe”, Phys. Rev. Let., vol. 94, 048101.
Svozil, K. (1993): “Randomness and Undecidability in Physics”, World Scientific.
Svozil, K., (1998): “Quantum Logic”, Springer, Singapore.
Tan, M.T., Tian, G-L., Ng, K.W., (2009): “Bayesian Missing Data Problems: EM, Data Augmentation and Noniterative Computation”, CRC Biostatistics Series, Chapman & Hall.
Tsuda I., (2015): “Chaotic itinerancy and its roles in cognitive neurodynamics, Current Opinion in Neurobiology”, Vol. 31, pg 67–71, SI: “Brain rhythms and dynamic coordination”.
Tsuda, I., (2001): “Toward an interpretation of dynamic neural activity in terms of chaotic dynamical systems”, Behav. Brain Sci., vol. 24, pp.793–810.
Tsuda, I., (2013), “Chaotic itinerancy”, Scholarpedia, 8(1):4459.
Tsuda, I. and Fujii, H., (2004): “A complex systems approach to an interpretation of dynamic brain activity I: chaotic itinerancy can provide a mathematical basis for information processing in cortical transitory and nonstationary dynamics.” , in: P. Érdi, A. Esposito, M. Marinaro, S. Scarpetta (Eds.) Computational Neuroscience: Cortical Dynamics, pp.109–128, Springer Berlin, Heidelberg.
Tsuda, I., (2009): “Hypotheses on the functional roles of chaotic transitory dynamics”. Chaos. Vol 19, pp.015113
West B., (2013): “Fractal Physiology, and Chaos in Medicine”, Word Scientific.
Wojcik, J., Clewley, R, Shilnikov, A.L., (2011): “Order parameter for bursting polyrhythms in multifunctional central pattern generators”. Phys. Rev. E. Vol. 83(5).
Wojcik J, Schwabedal J, Clewley R, Shilnikov A.L., (2014) “Key Bifurcations of Bursting Polyrhythms in 3-Cell Central Pattern Generators”. PLoS ONE 9(4): e92918. doi:10.1371/journal.pone.0092918 .
Zimmermann, H.-J., (1992): “Fuzzy Set Theory and Its Applications”. Springer Science+Business Media, New York.

![Figure 2. Chaos and Biological Information Processing. Adapted from [Nicolis J.S. & Tsuda, 1999]. “Outside” sends stimuli that can have more than one representations “Inside”. Categorization is possible due to coexisting attractors driven by a pacemaker in a “time-division-multiplexing-basis”. The whole process can be modelled as one of driven chaotic itinerancy. It can be implemented by very simple hardware giving rise to extremely complex software. Figure 2. Chaos and Biological Information Processing. Adapted from [Nicolis J.S. & Tsuda, 1999]. “Outside” sends stimuli that can have more than one representations “Inside”. Categorization is possible due to coexisting attractors driven by a pacemaker in a “time-division-multiplexing-basis”. The whole process can be modelled as one of driven chaotic itinerancy. It can be implemented by very simple hardware giving rise to extremely complex software.](http://operamedphys.org/sites/default/files/pictures/articles/2017_issue1_volume3/untitled folder/fig2.jpg)